空間図形の基本です。まずは空間における2直線の関係について見ていきますが、最初に平面をつくる条件について整理しておきます。
・平面を作る条件
空間図形を空間そのままで考えることも重要ですが、平面を取り出して平面図形に帰着させることが基本です。そこで、空間における平面がただ1つに定まる条件を整理すると次のようになります。
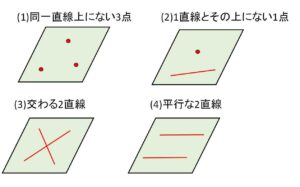
直線を含む場合は2個、点のみの場合は3個必要で(ただし同一直線上にあると直線1本になるのでダメ)、いずれも1つの要素だけでは決定できません。
平面がただ1つだけ決定されることはイメージでいうと、これらの条件で平面がグラグラせずに安定するということです。
また、これらの要素以上のものは同一平面上にあるとは限らないことになります(例えば4点など)。
・2直線の位置関係
空間における2直線の位置関係は次の3パターンになります。(i)(ii)は上記(3)(4)になるので、これらの場合には2直線はある平面上にあります。
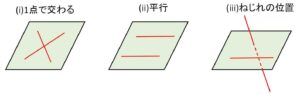
(iii)共有点をもたず、かつ平行でもない2直線は同じ平面上にはありません。このような2直線はねじれの位置にあるといいます。
(i)(ii)の場合には2直線が同一平面上にあるので、平面の場合と同じように2直線のなす角を決定できますが((ii)の場合は敢えて定めるなら\(0°\))、(iii)ねじれの位置の場合にはこのままだと2直線のなす角が決定できません。そこで直線を平行移動させて交わるようにしてなす角を決定します。
2直線\(l,m\)に対して、1点\(O\)を通る\(l,m\)にそれぞれ平行な直線\(l’,m’\)を引く。このとき点\(O\)のとりかたによらず\(l’,m’\)のなす角は等しくなり、この角\(θ\) (\(0°≦θ≦90°\)) を2直線\(l,m\)のなす角とする。特になす角が\(90°\)のとき、2直線は垂直であるという。
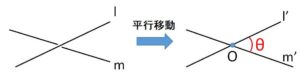
2直線が垂直の場合以外では、2直線が作る角は大きい角と小さい角の2種類が存在しますが、通常は小さい方の角(鋭角)を2直線のなす角とします。なお平行な直線のなす角を敢えて定めるなら\(0°\)とします。
また3直線の関係について空間においても平面の場合と同じことが成り立つ場合もありますし、空間においては成り立たない場合もあります。例えば3直線\(l,m,n\)について
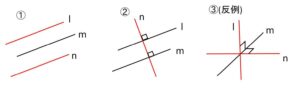
①\(l,m\)が平行、\(m,n\)が平行ならば、\(l,n\)は平行
②\(l,m\)が平行、\(n,l\)が垂直ならば、\(n,m\)は垂直
は空間においても成り立ちますが、
③\(l,m\)が垂直、\(m,n\)が垂直ならば、\(l,n\)は平行
は空間においては成り立ちません。反例は3直線が互いに垂直である場合などです。
これらのことは反例があるかどうかを意識しつつ、直線を色々動かして(回転・平行移動させる)、真偽を確かめることになります。
以上になります。お疲れ様です。
ここまで見て頂きありがとうございました。
next→空間図形の基本②(平面と直線、垂直二等分面) back→オイラーの定理(内心と外心の定理)