回転体について見ていきます。
・回転と円錐
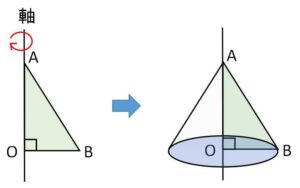
回転は点の回転が円になることを基本としつつ、上図のように直角三角形(内部も含む)を軸について回転させると円錐になることを主に利用します。線分\(AB\)の回転の場合はこの円錐の側面になります。
(例題)
一辺の長さ\(2\)の正四面体\(ABCD\)があり、辺\(AB\)の中点を\(M\)とする。
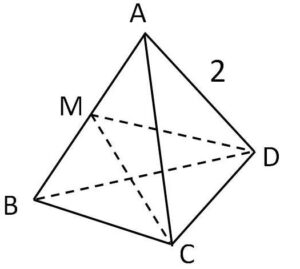
(1)辺\(AB\)を軸として、三角形\(ABC\)を一回転したときにできる立体の体積を求めよ。
(2)辺\(AB\)と平面\(CMD\)は垂直であることを示せ。
(3)辺\(AB\)を軸として、辺\(CD\)を一回転したときにできる図形の面積を求めよ。
(4)辺\(AB\)を軸として、三角形\(ACD\)を一回転したときに通過する部分の体積を求めよ。
(解答)
(1)
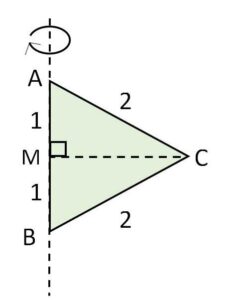
\(CM \perp AB\) より、回転してできる立体は円錐を2つくっつけたものである。
よって体積は
\(2\cdot\displaystyle\frac{1}{3}(\sqrt{3})^2π\cdot1=\)\(2π\)
(2)
((3)(4)の準備です)
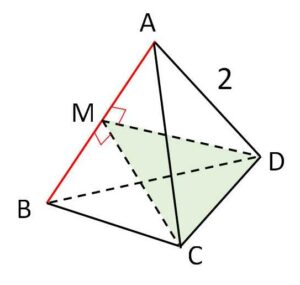
\(AB \perp CM\)、\(AB \perp DM\) だから
平面\(CMD\)と\(AB\)は垂直。
(3)
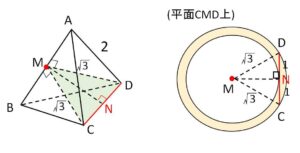
(2)より、平面\(CMD\)上で点\(M\)周りの線分\(CD\)の回転を考えればよい。
\(M\)から最も近い\(CD\)上の点は\(CD\)の中点\(N\)であり、最も遠い点は\(D\)(または\(C\))である。よって回転してできる図形は、\(MD\)を半径とする円から\(MN\)を半径とする円を除いた部分で、その面積は
\(π(MD^2-MN^2)=πND^2=π\cdot1^2=\)\(π\)
(補足)
\(ND\)と\(NC\)の回転によりできる図形は重複します(線分が半分になっても同じ図形ができる)。
(4)
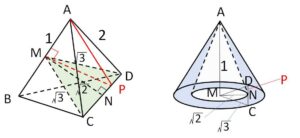
\(CD\)上に\(P\)をとると、(2)より\(P\)の位置によらず\(MP\)と\(AM\)は垂直である。よって、\(AP\)は\(AM\)を高さとする円錐面を作り、\(P\)を動かすことにより、\(△ACD\)の通過部分は右図のような円錐から円錐をくり抜いたものになることが分かる。ゆえに体積は
\(\displaystyle\frac{1}{3}(\sqrt{3})^2π\cdot1-\displaystyle\frac{1}{3}(\sqrt{2})^2π\cdot1\)
\(=\displaystyle\frac{1}{3}π\)
(補足)
これも\(△AND\)と\(△ANC\)の通過部分が重複しています(半分だけ回転させても同じ)。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→立体の面上における最短距離 back→体積比