立体の面上における最短距離の例題です。展開図を考えるのが基本です。
(例題)
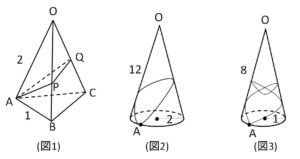
(1)図1のように、\(OA=OB=OC=2\)、\(AB=BC=CA=1\) である三角錐\(OABC\)がある。辺\(OB,OC\)上にそれぞれ点\(P,Q\)をとるとき、\(AP+PQ+QA\)の最小値を求めよ。
(2)図2,3のような円錐があり、底面の円周上に定点\(A\)をとる。\(A\)から始めて\(A\)で終わるように図2では1回、図3では2回糸を巻き付ける。このとき糸の長さの最小値をそれぞれ求めよ。
(解答)
(1)
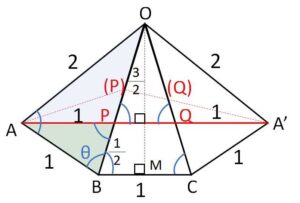
展開図において、\(AA’\)を結んだ線分の長さが最小値になる。
\(O\)から\(BC\)に垂線\(OM\)を下ろすと、\(OM\)について展開図は対称である。よって\(AA’//BC\)となるので、図の\(θ\)で表される角は全て等しい。
ゆえに \(AP=1\)
また \(△OAB∽△ABP\) より
\(BP=\displaystyle\frac{1}{2}\) だから
\(OP=\displaystyle\frac{3}{2}\)
よって \(PQ:BC=3:4\) となるから
\(PQ=\displaystyle\frac{3}{4}\)
したがって最小値は
\(1+\displaystyle\frac{3}{4}+1=\)\(\displaystyle\frac{11}{4}\)
(2)
(図2で1回巻き付ける場合)
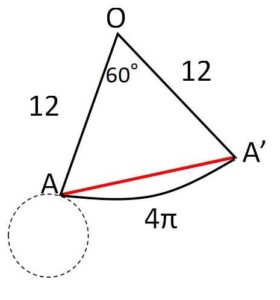
展開図のおうぎ形の中心角を\(x°\)とおくと
\(24π\cdot\displaystyle\frac{x}{360}=4π\)
\(x=60°\)
最短距離は\(AA’\)で、\(△OAA’\)は正三角形だから
\(12\)
(図3で2回巻き付ける場合)
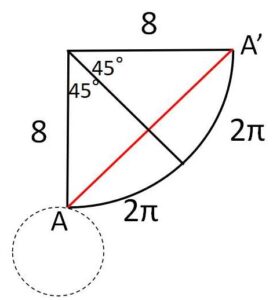
1つのおうぎ型(円錐の側面1つ分)の中心角を\(x°\)とすると
\(16π\cdot\displaystyle\frac{x}{360}=2π\)
\(x=45°\)
よって最短距離は\(AA’\)だから
\(8\sqrt{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間座標と空間図形 back→回転体