ここで立体問題の断面の取り出し方についてまとめておきます。
・空間図形における断面の取り出し方
空間図形ではその一部の平面を取り出して平面図形に帰着させるのが基本ですが、平面の取り出し方は無数に存在します。選び方はある程度は経験になってしまいますが、目安は次の通りです。
(1)対称な立体の場合は、対称面。
(2)球が絡む場合にはその球の中心を通る平面。すると球の断面は大円(球の半径と同じ円)になる。
(3)接する立体図形の場合には、接点を通る平面。
(その他)3点を通る平面は必ず存在するが、4点目についてはその平面に乗っているかどうかは一般的には不明。そこで、「平面上の2点を結ぶ直線上の点はその平面にある」ことや「平行な2面を平面で切断すると、それぞれの断面である直線は平行」などで取り出した平面上にあるかどうかを確認する。
実際に2つの例で検討してみます。
(例1)正四角錐の内接球の半径
内接球の半径なので(例1,2)いずれも立体を分割して「(全体の体積)=(分割した立体の体積の和)」より半径\(r\)を決定できます。ですがここでは立体図形の練習として断面を考えることで半径を求めてみます。
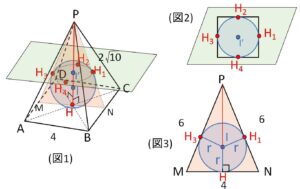
底面が一辺の長さ\(4\)の正方形、側面が\(2\sqrt{10},2\sqrt{10},4\)を三辺とする二等辺三角形である正四角錐\(P-ABCD\)の内接球の半径\(r\)を求めます。
まず球の中心\(I\)や各面との接点の位置を把握します。対称性より把握してももちろんよいですが、少し丁寧に考えてみます。
\(I\)は隣り合う2側面から等距離にあるので、角の二等分面\(PAC,PDB\)の交線である\(PH\)(\(H\)は正方形の対角線の交点)上にあります。
次に接点ですが\(PH\)は正四角錐の高さになるので、\(H\)は底面における接点です。
側面の接点が一番把握しにくいですが、底面に平行な断面を考えていくと、どこかに(図2)のような正方形に内接する円ができる断面があり、この円と正方形の接点が内接球と側面の接点です。よって側面の接点\(H_1~H_4\)は各二等辺三角形の\(P\)を通る中線上にあります。
(注)側面の接点は辺\(PA,PB,PC,PD\)上にはありません。もしこれらに接すると側面から球がはみ出てしまいます(これはこれで辺に接する球ではあるが)。また側面が傾いていることから側面の接点は球の中心\(I\)より少し上側にあります。
さて内接球の半径\(r\)を求めるために断面を取り出しますが、球の中心・接点・対称面を考慮すると、平面\(PMN\)が取り出す平面です(\(M,N\)は正方形の辺の中点)。
(図1)より
\(PN=\sqrt{(2\sqrt{10})^2-2^2}=6\)
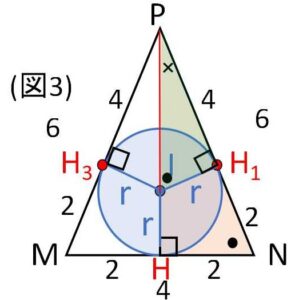
あとは(図3)の内接円の半径\(r\)(内接球の半径と同じ)を求めるだけです。
直角三角形の相似を利用することにすると、\(PH=4\sqrt{2}\) より
\(\displaystyle\frac{r}{4}=\displaystyle\frac{2}{4\sqrt{2}}\)
したがって
\(r=\sqrt{2}\)
(例2)正四面体の内接球の半径
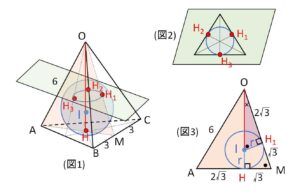
四面体\(OABC\)は一辺の長さ\(6\)の正四面体とすると、内接球の半径\(r\)は(例1)と同様に求めることができます。
まず球の中心\(I\)は、隣り合う2つの側面の角の二等分面上にあるので、3つの二等分面の交線である\(OH\)上にあります。\(H\)は正三角形の内心(外心、重心)であり、\(OH\)は正四面体の高さです。よって\(H\)は底面における接点で、他の側面も同じ正三角形からできているので向きを変えて考えれば、側面の接点\(H_1~H_3\)も各面の重心であることが分かります。((例1)と同様に底面に平行な断面で接点を通るものを考えると(図2)のようになります)
取り出す平面は、球の中心・接点を通るような平面\(OAM\)(\(M\)は\(BC\)の中点)で、ここでも辺\(OA(OB,OC)\)で接しないことに気を付けると、断面図は(図3)のようになります。
\(AM=OM=3\sqrt{3}\)
であり、\(H,H_1\)は重心であることから、接点までの線分の長さは図3のようになり、
\(OH=\sqrt{(3\sqrt{3})^2-(\sqrt{3})^2}=2\sqrt{6}\)
直角三角形の相似より
\(\displaystyle\frac{r}{2\sqrt{3}}=\displaystyle\frac{\sqrt{3}}{2\sqrt{6}}\)
\(r=\displaystyle\frac{\sqrt{6}}{2}\)
これは内接円の半径ですが、内接球の半径でもあります。
(例題)
1辺の長さが\(2a\)である正方形を底面とする正四角錐\(V\)に対し、底面上に中心をもち、\(V\)のすべての辺と接する球がある。このとき\(V\)の高さを求めよ。
(解答)
なお本問には直接関係ありませんが、球は正四角錐の面からは一部はみ出しています。
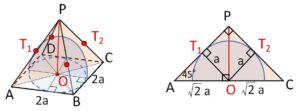
球の中心が底面上にあり正方形の辺に接することから、正方形に内接する円の半径\(a\)が球の半径。
平面\(PAC\)での断面を考えると、\(AO=\sqrt{2}a\) より
\(\angle T_1AO=45°\)
よって求める高さは
\(OP=OA=\)\(\sqrt{2}a\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→立体の共通部分 back→空間座標と空間図形