立体ができる条件の例題です。
(例題1)
三角錐\(ABCD\)において
\(AB=BC=CA=1\)、\(DA=DB=DC=d\)
が成り立っている。\(d\)のとりうる値の範囲を求めよ。
(解答)
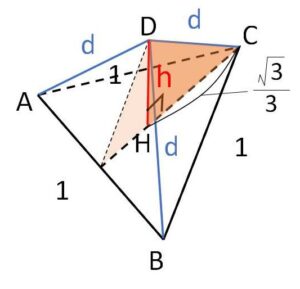
\(△ABC\)を底面として、三角錐の高さを\(DH=h\)とする。\(H\)は底面の外心(重心)であり、
\(CH=\displaystyle\frac{2}{3}\cdot\displaystyle\frac{\sqrt{3}}{2}=\displaystyle\frac{\sqrt{3}}{3}\)
よって
\(h^2=d^2-\displaystyle\frac{1}{3}\)
高さ\(h\)が\(0\)でない実数として存在すれば三角錐が存在するので
\(d>\displaystyle\frac{\sqrt{3}}{3}\)
(補足)
\(d\)が小さいうちは3線分\(DA,DB,DC\)が届かず、\(D\)が外心になるような\(d\)で初めて届く。このとき \(d=\displaystyle\frac{\sqrt{3}}{3}\) であるが、まだこれでは立体は作れない。この値より少しだけ大きければ立体を立ち上げることができて、\(d>\displaystyle\frac{\sqrt{3}}{3}\) が分かる。
もしくは、空間座標を使ってもよい。
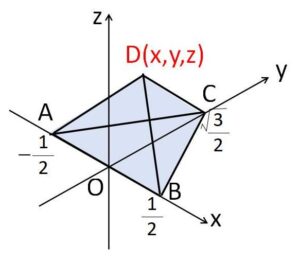
\(A(-\displaystyle\frac{1}{2},0,0),B(\displaystyle\frac{1}{2},0,0),C(0,\displaystyle\frac{\sqrt{3}}{2},0),\)\(D(x,y,z)\) とおくと
\(DA^2=DB^2=DC^2=d^2\) より
\((x+\displaystyle\frac{1}{2})^2+y^2+z^2=d^2\)・・・①
\((x-\displaystyle\frac{1}{2})^2+y^2+z^2=d^2\)・・・②
\(x^2+(y-\displaystyle\frac{\sqrt{3}}{2})^2+z^2=d^2\)・・・③
①-②や①-③などにより\(x,y,z^2\)を求めると
\(x=0,\ y=\displaystyle\frac{\sqrt{3}}{6},\ z^2=d^2-\displaystyle\frac{1}{3}\)
\(z\)が\(0\)でない実数ならば三角錐ができるので(\(0\)だと\(D\)が\(xy\)平面にのってしまう。虚数だと座標空間上に存在しない)
\(d^2-\displaystyle\frac{1}{3}>0\)
\(d>\displaystyle\frac{\sqrt{3}}{3}\)
(例題2)
四点\(A,B,C,D\)を頂点とする四面体において、各辺の長さは
\(AB=x\)、\(AC=AD=BC=BD=5\)、\(CD=4\)
である。このような四面体が存在するような\(x\)の範囲を求めよ。
(解答)
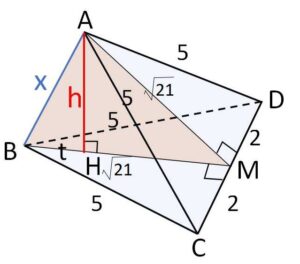
\(CD\)の中点を\(M\)とすれば、\(AC=AD\) より\(A\)から平面\(BCD\)に下ろした垂線の足\(H\)は\(BM\)上にある。
\(AH=h\)、\(BH=t\) とおくと、\(HM=\sqrt{21}-t\) だから
\(h^2=x^2-t^2\)・・・(1)
\(h^2=21-(\sqrt{21}-t)^2\)・・・(2)
(1)(2)より
\(t=\displaystyle\frac{x^2}{2\sqrt{21}}\)
(1)より
\(h^2=x^2-\displaystyle\frac{x^4}{84}=\displaystyle\frac{x^2}{84}(84-x^2)\)
\(h\)が\(0\)でない実数をとればよいので
\(84-x^2>0\)
\(x>0\)もあわせて
\(0<x<2\sqrt{21}\)
(補足)
\(△ABM\)が存在すれば高さも存在するので、\(△ABM\)の成立条件を考えてもよい。
\(|\sqrt{21}-\sqrt{21}|<x<\sqrt{21}+\sqrt{21}\)
\(0<x<2\sqrt{21}\)
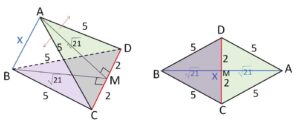
または図で\(CD\)を軸として二等辺三角形\(CAD\)を回転させて\(x\)を変化させてみると、\(△CAD\)と\(△CBD\)が重なるところから開ききるところの間で四面体ができるので
\(0<x<2\sqrt{21}\)
と考えることもできる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間における3つのなす角の制限 back→立体の共通部分