空間における3半直線のなす角の制限についてです。
(例題)
空間上に4点\(O,A,B,C\)があり、\(OA=OB=OC=1\)、\(\angle AOB=60°\)、\(\angle AOC=90°\) を満たしている。このとき \(\angle BOC\) のとりうる値の範囲を求めよ。(角は\(0°\)以上\(180°\)以下とする)
1つの角をつくる2線分を固定して(これだけなら一般性を失わない。1つ目の角だけ空間座標の\(xy\)平面に固定するのと同じ)、2つ目の角が一定になるように空間上で動かして(円錐を作って)考えます。
(例題)
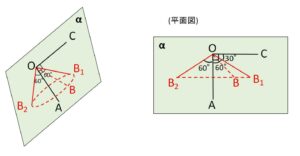
\(90°\)のなす角を作る\(A,O,C\)をある平面\(α\)に固定して考える。
\(\angle AOB=60°\) を満たすように\(B\)を動かすと円錐の側面を作る。\(α\)の垂線方向から見ると右上図のようになり、\(B\)が平面\(α\)上の\(B_1,B_2\)に位置するときに\(\angle BOC\)は最小・最大値をとる。・・・(注)
よって
\(90°-60°≦\angle BOC≦90°+60°\)
\(30°≦\angle BOC≦150°\)
(注)
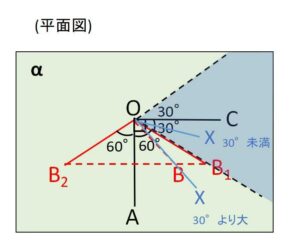
円錐の側面を作るように\(B\)をぐるぐる回転させると、\(B\)が図の\(B_1,B_2\)のときに\(\angle BOC\)が最小最大になることはなんとなく分かると思いますが、全体の立体図を平面\(α\)の垂線方向から見て平面化することで説明がつきます。例えば最小値だと、\(\angle B_1OC\ (=30°)\)のほうを\(OC\)を軸として回転させるとこれも円錐面になりますが、円錐の外側にある点\(X\)では \(\angle XOC>30°\) となります。\(B_1\)以外の\(B\)は円錐の外側にあるので\(30°\)が最小値です。最大値についても同様に考えることができます。
(参考)ベクトルで考えると機械的に処理が可能です。
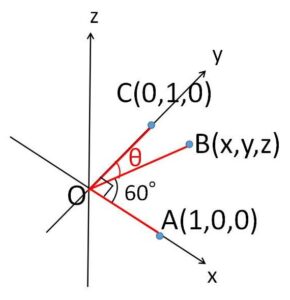
\(O\)を原点、\(A(1,0,0),C(0,1,0),B(x,y,z)\)として、\(\angle BOC=θ\) とすれば、使っていない条件 \(OB=1\)、\(\angle AOB=60°\) より
\(x^2+y^2+z^2=1\)・・・①
\(x=1\cdot1\cdot\cos60°\)・・・②
\(y=1\cdot1\cdot\cosθ\)・・・③
②③より \(x,y\)は実数で、これらを①に代入して
\(\displaystyle\frac{1}{4}+\cos^2θ+z^2=1\)
\(z^2=\displaystyle\frac{3}{4}-\cos^2θ\)
\(z\)が実数であるためには
\(\displaystyle\frac{3}{4}-\cos^2θ≧0\)
よって
\(-\displaystyle\frac{\sqrt{3}}{2}≦\cosθ≦\displaystyle\frac{\sqrt{3}}{2}\)
したがって
\(30°≦θ≦150°\)
と分かります。
※一般的に3つの角の制限について考えると次のようになる。
3半直線\(OA,OB,OC\)のなす角を \(\angle AOB=γ\)、\(\angle BOC=α\)、\(\angle COA=β\) (いずれの角も \(0°≦α,β,γ≦180°\)) とすると
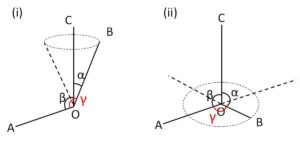
(i)\(0°≦α+β≦180°\) のとき
\(|α-β|≦γ≦α+β\)
(ii)\(180°≦α+β≦360°\) のとき
\(|α-β|≦γ≦360°-(α+β)\)
例題では(i)のケースになります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
back→立体ができる条件