空間図形の基本③(2平面)

今回は2平面の関係です。

・2平面の関係
2平面の位置関係は次の2パターン(一致を含めれば3パターン)になります。

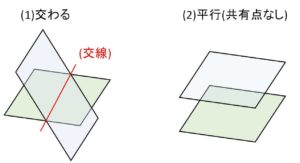
(1)交わる場合には、共有点全体は直線となりこの直線を2平面の交線とよびます。交わりが直線になるのは、平面が直線を平行移動してできることから分かります。

・2平面のなす角
平面が交わる場合(上記(1))、2平面は何らかの角度を成して交わっています。そこで2平面のなす角を次のように定義します。

(2平面のなす角)
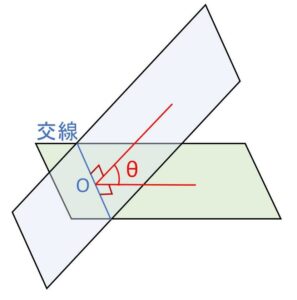
交わる2平面の交線上の点\(O\)から、各平面上に交線に垂直に直線を引く。これら2直線のなす角を2平面のなす角といい、特になす角が\(90°\)の場合、2平面は垂直であるという。

交線上の点\(O\)のとりかたによらず、なす角は同じです。また通常なす角\(θ\)は \(0°<θ≦90°\) の範囲にとります。(平行な場合\(θ=0°\)とすることもある)

以上になります。お疲れ様です。
ここまで見て頂きありがとうございました。
next→立体の断面　back→空間図形の基本②(平面と直線・垂直二等分面)