正多面体の種類について見ていきます。
・正多面体の種類
三角柱や四角錐のようないくつか平面(多角形)で囲まれてできる立体を多面体といいます。多面体のうち凹み(へこみ)のない多面体を凸多面体(とつためんたい)といいます。(もう少し明確にすると、どの2頂点を結んでも、その線分が多面体に含まれるときつまり外部を通らないとき、凸多面体という)
さらに凸多面体のうち、次の2つの条件を満たすものを正多面体といいます。
(1)各面は全て合同な正多角形
(2)各頂点に集まる面の数がすべて等しい
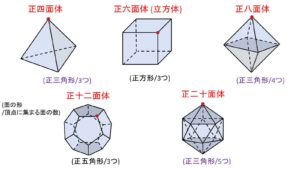
これらの条件を満たすもの、つまり正多面体は全部で下図の5種類しかありません。各立体の名称の漢数字は面の数を表しています。
(解説)
まず(1)の条件に着目すると各面の正多角形は、「正三角形、正方形、正五角形、正六角形・・・」と考えられますが、
・立体を作るには1つの頂点に最低3つの面を集める必要があることと
・1点を共有するように平面上に正多角形を並べたときにその点まわりに角の和が\(360°\)以上になってしまうと凸である立体を作ることができない(\(360°\)でもダメ)
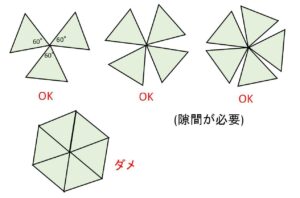
ことに着目します。正六角形の1内角は\(120°\)なので、\(120°×3=360°\) より正多角形の面にはできず、正七角形以上ではさらに内角が大きくなるので、正多角形の面にできるのは「正三角形、正方形、正五角形」のみになることが分かります。これらの内角は\(60°,90°,108°\)なので、\(360°\)以上にならないようにするには
・正三角形→1頂点に集まる面の数は、3,4,5の3パターン
・正方形→1頂点に集まる面の数は3のみ
・正五角形→1頂点に集まる面の数は3のみ
となり全部で5パターンです。次に (2)頂点に集まる面の数が等しい ことに着目して多面体を組み立ててみると、
(面が正三角形)
(i)頂点に集まる面が3つ
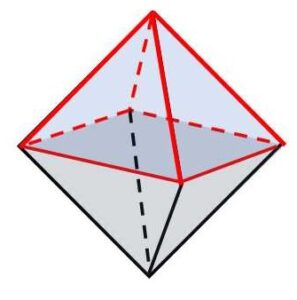
最初に3つの正三角形で立体を部分的に作ると、各頂点に3つ面が集まるようにするには、1つの正三角形を追加して閉じるしかないので、全部で4面になり正四面体ができる。よって例えば正四面体を2つくっつけた下図の多面体はすべての面が正三角形ですが、4つの面が集まる頂点もあるので正多面体ではありません。
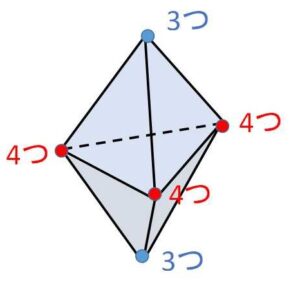
(ii)頂点に集まる面が4つ
(この辺りから複雑になってくるのでオイラーの多面体定理(次回扱います)を用いて面の数を確定させてしまったほうがよいかもしれません)
まず4つの正三角形で底が無い四角錐のような立体を作り、残りの部分で頂点に集まる面が4つであるようにするには、底の4本の辺にそれぞれ1つずつ正三角形をくっつけて立体を閉じるしかないので、全部で8面になり正八面体ができます。
(iii)頂点に集まる面が5つ
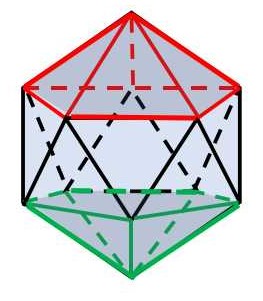
まず5つの正三角形で底が無い五角錐のような立体を作る。各頂点に集まる面の数が5つになるようにするには、底の5辺に1枚ずつ正三角形をくっつけ、さらにこのくっつけた5枚の正三角形の間にも1枚ずつ計5枚の正三角形をくっつける必要がある。これら10枚の正三角形は交互に逆向きになっていて、穴が開いている底は5角形状になっているので、5つ正三角形をくっつけて閉じれば立体が完成する。面の数は合計 \(5+10+5=20\) になるので、正二十面体。
(面が正方角形)
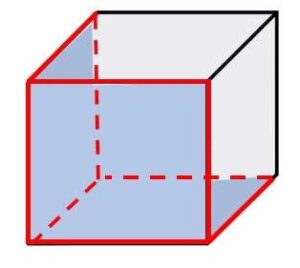
頂点に集まる面の数は3枚。3つの正方形で部分的に立体を作ると、さらに3枚の正方形を追加して立体を閉じることになるので、全部で6面。よって正六面体(立方体)になる。
(面が正五角形)
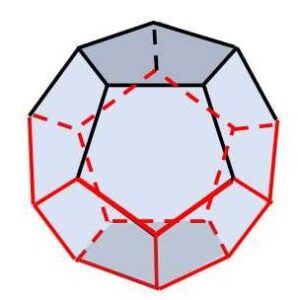
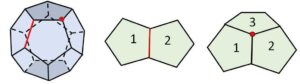
頂点に集まる面の数は3枚。1つの正五角形を置くと、5辺に正五角形を1つずつくっつけることになる。さらに5枚の正五角形をくっつけて、1枚の正五角形で立体を閉じればよい。合計 \(1+5+5+1=12\) 個の面になり、正十二面体。
・正多面体の辺と頂点の数
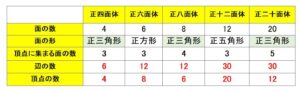
正多面体の面の形と頂点に集まる面の数をまとめると次の通りです。
正四面体: (正三角形,3つ)
正六面体: (正方形,3つ)
正八面体: (正三角形,4つ)
正十二面体: (正五角形,3つ)
正二十面体: (正三角形,5つ)
次に辺の数と頂点の数を考えてみます。正八面体くらいまでなら数えたほうが早そうですが、正十二面体と正二十面体では数え間違えも起きる可能性がでてくるので、計算で求めたほうがよいです。
(正十二面体)
まず辺の数。正五角形が12面あるので、\(5×12=60\)。しかしこのままだと1辺は2つの面に共有されていることから2重にカウントされている。よって辺の数は \((5×12)÷2=30\) 本。
頂点の数も同様に考えると、1頂点が3つの面で共有されているので \((5×12)÷3=20\) 個。
(正二十面体)
正十二面体と同じ考えで求めることができる。正三角形が20面あるが、辺の数は同じく1辺が2つの面で共有されているので \((3×20)÷2=30\) 本。
頂点の個数は、1頂点が5つの面で共有されているから \((3×20)÷5=12\) 個。
他の正多面体についても計算するか直接数えるかで求めて、まとめると次のようになります。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→オイラーの多面体定理 back→三垂線の定理