空間ベクトルの基礎的な内容にについて見ていきます。
・空間ベクトルの定義
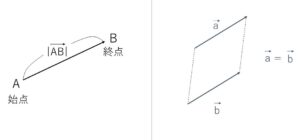
平面の場合と同様に、空間における有向線分について、その位置を問題にせず、向きと長さ(大きさ)だけに着目したものを空間ベクトルといいます。
有向線分\(AB\)と同じ向き、大きさをもったベクトルを\(\overrightarrow{AB}\)と書き、\(A\)を始点、\(B\)を終点、\(\overrightarrow{AB}\)の大きさを\(|\overrightarrow{AB}|\)で表します。特に大きさが\(1\)であるベクトルを単位ベクトルといいます。(\(\vec{a}\)のように1文字でベクトルを表す場合もあります)
図のように位置が違っていても向きと大きさが同じ2つのベクトル\(\vec{a},\vec{b}\)は同じものになります。
このとき2つのベクトル\(\vec{a},\vec{b}\)は等しいといい、\(\vec{a}=\vec{b}\) で表します。
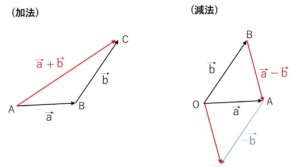
また空間ベクトルにおける、ベクトルの「加法\(\vec{a}+\vec{b}\)・減法\(\vec{a}-\vec{b}\)・逆ベクトル\(-\vec{a}\)・零ベクトル\(\vec{0}\)・ベクトルの実数倍\(k\vec{a}\)」は平面ベクトルと同じに内容になります。
\(\overrightarrow{A□}+\overrightarrow{□C}=\overrightarrow{AC}\)
\(\overrightarrow{□A}-\overrightarrow{□B}=\overrightarrow{BA}\)
も相変わらず重要公式になります。
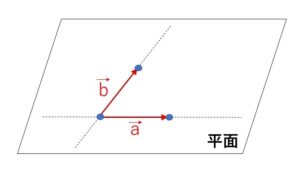
空間における3点は、一直線上にない場合にはこの3点を通る平面が存在します。
2つの空間ベクトルは始点や終点を揃えることにより、登場する点を最大3点にすることができるので、2つのベクトルを平面に乗せることができます。また2つのベクトル方向の軸(直線)を考えれば、この2つのベクトルの実数倍や和・差をとったものもこの平面上に乗ることになるので、2つのベクトルしか登場しない場合には平面で考えればよいことになります。
(3点が一直線上にある場合には平面以下の直線や点の世界になります。よって2つのベクトルの場合最大の2次元である平面で考えればよい)
・空間ベクトルの演算
空間ベクトルにおいても、平面ベクトルと同じ演算法則が成り立ちます。
(1)\(\vec{a}+\vec{b}=\vec{b}+\vec{a}\) (交換法則)
(2)\((\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})\) (結合法則)
(3)\(\vec{a}+\vec{0}=\vec{a}\)
(4)\(\vec{a}+(-\vec{a})=\vec{a}-\vec{a}=\vec{0}\)
(実数倍)
\(k,l\)を実数として
(5)\(k(l\vec{a})=(kl)\vec{a}\)
(6)\((k+l)\vec{a}=k\vec{a}+l\vec{a}\)
(7)\(k(\vec{a}+\vec{b})=k\vec{a}+k\vec{b}\)
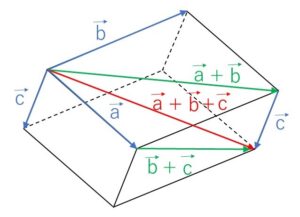
(2)だけ3つのベクトルが登場するので図示しておきます。
図のように\(\vec{a},\vec{b},\vec{c}\)で作られる平行六面体(向かい合った3組の面がそれぞれ平行な六面体。すべての面が平行四辺形で対面は合同になる)を考えると成り立つことが分かります。
(例題)
図の正八面体において、\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(\overrightarrow{OC}=\vec{c}\) とするとき、次のベクトルを\(\vec{a},\vec{b},\vec{c}\)で表せ。
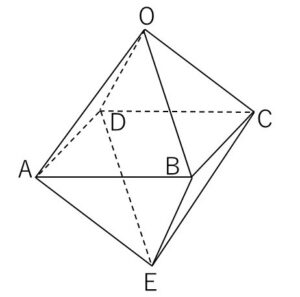
(1)\(\overrightarrow{CE}\) (2)\(\overrightarrow{OD}\) (3)\(\overrightarrow{OE}\)
まず水平の切断面、四角形\(ABCD\)は正方形。また対称的な立体なので縦方向の切断面、四角形\(ODEB\)、\(OAEC\)も同じく正方形です。したがって\(\vec{a},\vec{b},\vec{c},\overrightarrow{OD}\)と同じベクトルが下側の4辺にも表れます。
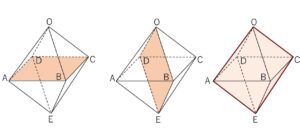
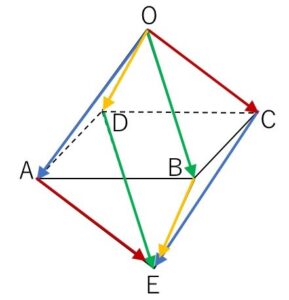
(解答)
(1)
\(\overrightarrow{CE}=\overrightarrow{OA}\)\(=\vec{a}\)
(2)
(\(C\)を経由すると)
\(\overrightarrow{OD}=\overrightarrow{OC}+\overrightarrow{CD}\)
\(=\overrightarrow{OC}+\overrightarrow{BA}\)
\(=\overrightarrow{OC}+(\overrightarrow{OA}-\overrightarrow{OB})\)
\(=\vec{a}-\vec{b}+\vec{c}\)
(3)
\(\overrightarrow{OE}=\overrightarrow{OA}+\overrightarrow{AE}\)
\(=\overrightarrow{OA}+\overrightarrow{OC}\)
\(=\vec{a}+\vec{c}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間ベクトルの成分 back→空間における距離