折れ線の長さ | 教えて数学理科

空間における折れ線の長さの最小値問題について見ていきます。

平面のときと同じで対称な点がポイントになります。
また円を考えて、ある点を他の点に置き換えることも重要です。

(例題1)
2点 \(A(5,0,9)\), \(B(1,4,3)\) と\(xy\)平面上を動く点\(P\)に対して、\(AP+PB\)の最小値を求めよ。

\(A,B\)の\(z\)座標の符号が同じなので、\(xy\)平面に対して同じ側にあります。
このままだと折れ線になるので、どちらかを\(xy\)平面について対称移動させた点を考えることになりますが、\(B\)を対称移動させた点を\(B’\)とすれば、\(AP+PB=AP+PB’\)です(注参照)。あとは\(A,P,B’\)が一直線にあるときを考えると、このとき最小となります。

(解答)

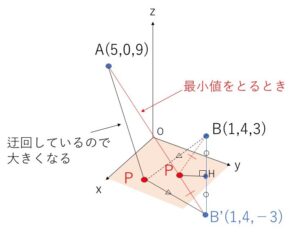
空間折れ線例題1-1

\(B(1,4,3)\)を\(xy\)平面に関して対称移動した点を\(B’\)とすると、\(B'(1,4,-3)\)

また、\(AP+PB=AP+PB’\) なので、最小となるときは\(A,P,B’\)が一直線上にあるときになる。

よって、\(AP+PB\)の最小値は\(AB’\)となるから、\(A(5,0,9)\) より

(最小値)\(=\sqrt{(-4)^2+4^2+(-12)^2}\)
\(=4\sqrt{11}\)

(注)\(PB=PB’\)について

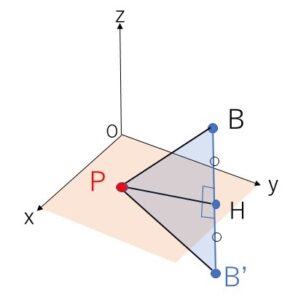
空間折れ線例題1-2

\(B,B’\)は\(xy\)平面について対称な点なので、\(BB’\)と\(xy\)平面との交点を\(H\)とすれば、\(H\)は\(B,B’\)から下した垂線の足になる。よって任意の\(H\)を通る\(xy\)平面上の直線と、\(BB’\)は垂直となるから、任意の\(xy\)平面上の点\(P\)について

\(\angle PHB=\angle PHB’=90°\)

また \(HB=HB’\)

よって\(△PHB\)と\(△PHB’\)は、
「\(PH\)共通、\(HB=HB’\)、はさまれる角が\(90°\)で同じ」となることから合同。

したがって \(PB=PB’\) となります。

もしくは、直角三角形になることから三平方の定理より
\(PB=\sqrt{PH^2+HB^2}\)
\(PB’=\sqrt{PH^2+HB’^2}\)
そして、\(HB=HB’\) だから、\(PB=PB’\) と結論づけてもよいです。

(例題2)
座標空間において、点 \(A(1,0,2)\), \(B(0,1,1)\) とする。
(1)\(yz\)平面における、原点を中心とする半径\(\sqrt{2}\)の円と\(z\)軸の交点のうち、\(z\)座標が負の値になるものを\(Q\)とする。\(Q\)の\(z\)座標を求めよ。
(2)点\(P\)を\(x\)軸上を動く点とするとき、\(AP+PB\)の最小値を求めよ。

今回は\(P\)が軸上を動くケースです。この場合は(1)のように円を考えることになります。

(解答)

\(z=-\sqrt{2}\) とすぐにわかりますが、(2)を踏まえたポイントはこの円上に\(B(0,1,1)\)があることです。

(1)

空間折れ線　例題2-1

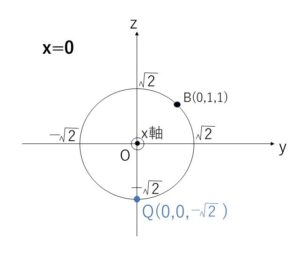
\(Q\)の\(z\)座標は　\(z=-\sqrt{2}\)

(2)

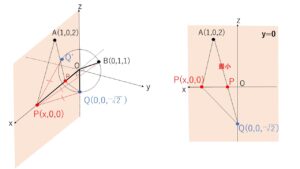
\(OP\)を高さとする円錐を考えると分かりやすいですが
\(PB=\sqrt{OP^2+OB^2}\), \(PQ=\sqrt{OP^2+OQ^2}\) で、\(B,Q\)は半径\(\sqrt{2}\)の円周上にあるから、\(OQ=OB\)。よって\(PB=PQ\)です(ほかの円周上の点\(Q’\)についても、\(PB=PQ’\)となりますがこの問題では使いません)。円錐を考えると、\(PB,PQ\)はちょうど母線になっています。
したがって、\(B\)は\(Q\)に置き換えることができて、\(A,Q,P\)はちょうど同じ平面(\(zx\)平面)上の点なので、あとはただの平面における折れ線の最小値を求める問題です。
誘導で\(Q\)がちょうど同じ平面にあるようにうまく設定されていますが、誘導が無い場合には円周上の点で同じ平面にのるような点を探すことになります。
また、点\(A,B\)のどちらを通る円を考えるかという点については解答後に説明します。

\(PB=\sqrt{OP^2+OB^2}\), \(PQ=\sqrt{OP^2+OQ^2}\)
\(OQ=OB\) より
\(PB=PQ\)

よって
\(AP+PB=AP+PQ\)

また、\(A,P,Q\)の\(y\)座標は\(0\)なので、この3点は\(zx\)平面上にある。
この平面上で\(AP+PQ\)が最小値をとるときを考えると、それは\(A,P,Q\)が一直線上にあるときで、このとき最小値は\(AQ\)

したがって \(A(1,0,2)\), \(Q(0,0,-\sqrt{2})\) より
(\(AP+PB\)の最小値)
\(=AQ\)
\(=\sqrt{1^2+0^2+(2+\sqrt{2})^2}\)
\(=\sqrt{7+4\sqrt{2}}\)

\(A,B\)のどちらを通る円を考えるかは、\(P\)が動く軸が「円を含む平面に垂直」になるかどうかで判断します(軸が円錐の高さになるほうを選ぶということです)。この例題では\(P\)が\(x\)軸を動くために、この軸と垂直な平面である\(yz\)平面での円を考えることになります。したがって\(yz\)平面にある\(B\)のほうを通る円を考えます。

(参考別解)
\(P(x,0,0)\) とおくと \(A(1,0,2)\), \(B(0,1,1)\) より
\(AP+PB\)
\(=\sqrt{(x-1)^2+2^2}+\sqrt{x^2+1^2+1^2}\)
\(=\sqrt{(x-1)^2+(0-2)^2}+\sqrt{(x-0)^2+\{0-(-\sqrt{2})\}^2}\)・・・(※)

\(xy\)平面上で
\(R(x,0)\), \(C(1,2)\), \(D(0,-\sqrt{2})\) とすると

(※)\(=CR+RD\)

よって最小値は\(C,R,D\) が一直線上にあるときで
(図は本解答の右側の平面図で\(z\)軸が\(y\)軸に変わるだけで同じになる)

(最小値)\(=CD\)\(=\sqrt{1^2+(2+\sqrt{2})^2}\)
\(=\sqrt{7+4\sqrt{2}}\)

ちなみに微分を利用すると相当面倒になります。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→複数のベクトルのなす角　 back→ベクトルの大きさ