空間上の点\(P\)のベクトルについての等式が与えられた際の、\(P\)の位置を求める例題です。
解き方は平面のときと同様になります。また、ついでに体積比についても扱っていきます。
(例題)
四面体\(OABC\)に関して、\(2\overrightarrow{OP}+3\overrightarrow{AP}+5\overrightarrow{BP}+7\overrightarrow{CP}=\vec{0}\) が成り立っている。
(1)点\(P\)はどのような位置にあるか。
(2)4つの四面体 \(PABC\), \(PBCO\), \(PCOA\), \(POAB\) の体積の比を求めよ。
(解答)
(1)
\(2\overrightarrow{OP}+3\overrightarrow{AP}+5\overrightarrow{BP}+7\overrightarrow{CP}=\vec{0}\) より
\(2\overrightarrow{OP}+3(\overrightarrow{OP}-\overrightarrow{OA})+5(\overrightarrow{OP}-\overrightarrow{OB})+7(\overrightarrow{OP}-\overrightarrow{OC})=\vec{0}\)
(\(P\)に関する情報が知りたいので、\(\overrightarrow{OP}=\cdots\) の形にする)
よって
\(\overrightarrow{OP}=\displaystyle\frac{3\overrightarrow{OA}+5\overrightarrow{OB}+7\overrightarrow{OC}}{17}\)
(式の簡略化のため位置ベクトルを導入します)
ここで\(O\)を基準として
\(P(\vec{p})\), \(A(\vec{a})\), \(B(\vec{b})\), \(C(\vec{c})\) とおくと
\(\vec{p}=\displaystyle\frac{3\vec{a}+5\vec{b}+7\vec{c}}{17}\)
3つのベクトルのうち、\(\vec{b},\vec{c}\) の部分に着目すると(他の組合せでもよいです。後で説明します)
\(5\vec{b}+7\vec{c}=\displaystyle\frac{5\vec{b}+7\vec{c}}{7+5}×12\) です。
\(\vec{d}=\displaystyle\frac{5\vec{b}+7\vec{c}}{7+5}\) とでもおくと、\(D(\vec{d})\) は線分\(BC\)を\(7:5\)の比に内分する点になっています。そして今度はこの\(\vec{d}\)と残りの\(\vec{a}\)について同じ式変形をします。
\(\vec{p}=\displaystyle\frac{3\vec{a}+5\vec{b}+7\vec{c}}{17}\)
\(=\displaystyle\frac{3\vec{a}+12\cdot\displaystyle\frac{5\vec{b}+7\vec{c}}{7+5}}{17}\)
ここで、\(\vec{d}=\displaystyle\frac{5\vec{b}+7\vec{c}}{7+5}\) とおくと、\(D(\vec{d})\) は線分\(BC\)を\(7:5\)の比に内分する点である。
\(\vec{p}=\displaystyle\frac{3\vec{a}+12\vec{d}}{17}\)
\(=\displaystyle\frac{15}{17}\cdot\displaystyle\frac{3\vec{a}+12\vec{d}}{12+3}\)
\(=\displaystyle\frac{15}{17}\cdot\displaystyle\frac{\vec{a}+4\vec{d}}{4+1}\)
\(\vec{t}=\displaystyle\frac{\vec{a}+4\vec{d}}{4+1}\) とおくと、\(T(\vec{t})\)は線分\(AD\)を\(4:1\)の比に内部する点である。
したがって
\(\vec{p}=\displaystyle\frac{15}{17}\vec{t}\) となるから、\(P\)は線分\(OT\)を\(15:2\)の比に内分する点になる。
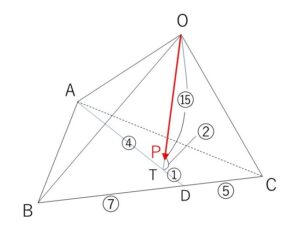
以上から
線分\(BC\)を\(7:5\)の比に内分する点を\(D\)、線分\(AD\)を\(4:1\)の比に内分する点を\(T\)とすると、点\(P\)は線分\(OT\)を\(15:2\)の比に内分する点である。
また、解答では最初に \(\vec{b},\vec{c}\) についてまとめましたが、\(\vec{a},\vec{b}\) or \(\vec{a},\vec{c}\) についてまとめてもよいです。ただし答えの表記方法が若干変わります。
(2)
(i)底面積が共通ならば、(体積比)=(高さの比)
(ii)高さが共通ならば、(体積比)=(底面積の比)
です。(1)で求めた比を駆使して高さの比や底面積の比を考えていきます。高さの比を考えるときは底面に垂線を下すことがポイントになります。なお解答では最初に底面積の比をまとめて出しておきます。
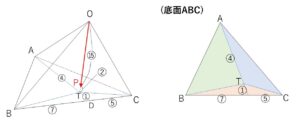
\(△TBC=\displaystyle\frac{1}{5}△ABC\)
\(△TCA=\displaystyle\frac{5}{12}\cdot\displaystyle\frac{4}{5}△ABC=\displaystyle\frac{1}{3}\)
\(△TAB=\displaystyle\frac{7}{12}\cdot\displaystyle\frac{4}{5}△ABC=\displaystyle\frac{7}{15}\)
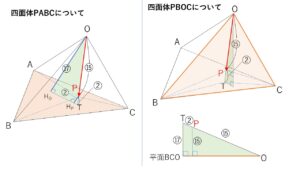
続いて高さの比を考えていきます。全体の四面体\(OABC\)を基準として
まず四面体\(PABC\)ですが、底面は\(△ABC\)で共通なので高さの比が体積比なり、\(O\)と\(P\)から平面\(ABC\)に垂線を下してその足をそれぞれ\(H_O,H_P\)とおくと、\(OH_O:PH_P=17:2\) になります。したがって\(OABC\)との体積比も\(17:2\)です。
残りの3つの四面体については、高さの比→底面積の比と2段階で考えます。例えば、四面体\(PBCO\)はまず四面体\(TBCO\)と比べると、底面を\(△BCO\)とすると共通で、\(T,P\)から平面\(BCO\)に垂線を下ろすと高さの比が\(17:15\)になり、さらに\(TBCO\)と\(OABC\)の比は、高さが共通(\(OH_O\))なので先ほど求めた底面積の比が体積比になります。
ここで、四面体\(OABC\)の体積を\(V\)とし、4つの四面体 \(PABC\), \(PBCO\), \(PCOA\), \(POAB\) の体積をそれぞれ\(V_1~V_4\)とおくと
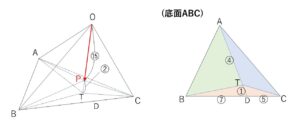
\(V_1\)については四面体\(OABC\)と比べて、底面を\(△ABC\)とすると共通で、\(TO:TP=17:2\) より \((OABCの高さ):(PABCの高さ)=17:2\) となるから
\(V_1=\displaystyle\frac{2}{17}V\)
\(V_2\)については四面体\(TBCO\)とまず比べて、底面を\(△BCO\)とすると共通で、\(OT:OP=17:15\) より \((TBCOの高さ):(PBCOの高さ)=17:15\) となるから
\(V_2=\displaystyle\frac{15}{17}(四面体TBCO)\)
続いて、四面体\(TBCO\)と四面体\(OABC\)を比べると、高さが共通で \(△TBC=\displaystyle\frac{1}{5}△ABC\) より、\((OABCの底面積):(TBCOの底面積)=5:1\) となるから
\((四面体TBCO)=\displaystyle\frac{1}{5}V\)
したがって
\(V_2=\displaystyle\frac{15}{17}\cdot\displaystyle\frac{1}{5}V\)\(=\displaystyle\frac{3}{17}V\)
\(V_3,V_4\)についても同様に考えると
\(V_3=\displaystyle\frac{15}{17}\cdot\displaystyle\frac{1}{3}V\)\(=\displaystyle\frac{5}{17}V\)
\(V_4=\displaystyle\frac{15}{17}\cdot\displaystyle\frac{7}{15}V\)\(=\displaystyle\frac{7}{17}V\)
したがって4つの四面体の体積は
\(\displaystyle\frac{2}{17}V:\displaystyle\frac{3}{17}V:\displaystyle\frac{5}{17}V:\displaystyle\frac{7}{17}V=\)\(2:3:5:7\)
\(2\overrightarrow{OP}+3\overrightarrow{AP}+5\overrightarrow{BP}+7\overrightarrow{CP}=\vec{0}\)
のちょうど係数になっています(一般的に係数比が体積比となります)。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→同一直線上にある条件 back→空間の位置ベクトルと分点・重心