交点に関するベクトルを求める問題や、点の一致に関する問題について見ていきます。
(例題1)
四面体\(OABC\)において辺\(AB\)の中点を\(E\)、辺\(OC\)を\(2:1\)に内分する点を\(F\)、辺\(OA\)を\(1:2\)に内分する点を\(P\)とする。また、\(Q\)を \(\overrightarrow{BQ}=t\overrightarrow{BC}\) を満たす辺\(BC\)上の点とする。\(PQ\)と\(EF\)が交わるとき、実数\(t\)の値を求めよ。また、\(PQ\)と\(EF\)の交点を\(X\)とするとき、\(\overrightarrow{OX}\)を\(\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}\)で表せ。
(解答)
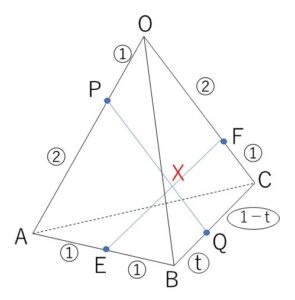
\(Q\)は辺\(BC\)上の点だから \(0<t<1\)
\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(\overrightarrow{OC}=\vec{c}\) とおくと
交点\(X\)は\(EF\)上にあることから、実数\(k\)を用いると
\(\overrightarrow{OX}=(1-k)\overrightarrow{OE}+k\overrightarrow{OF}\)
\(=(1-k)\cdot\displaystyle\frac{\vec{a}+\vec{b}}{2}+k\cdot\displaystyle\frac{2}{3}\vec{c}\)
\(=\displaystyle\frac{1-k}{2}\vec{a}+\displaystyle\frac{1-k}{2}\vec{b}+\displaystyle\frac{2}{3}k\vec{c}\)・・・①
また\(X\)は\(PQ\)上にもあるから、実数\(h\)を用いると
\(\overrightarrow{OX}=(1-h)\overrightarrow{OP}+h\overrightarrow{OQ}\)
\(=(1-h)\cdot\displaystyle\frac{1}{3}\vec{a}+h\{(1-t)\vec{b}+t\vec{c}\}\)
\(=\displaystyle\frac{1-h}{3}\vec{a}+h(1-t)\vec{b}+ht\vec{c}\)・・・②
\(\vec{a},\vec{b},\vec{c}\) は1次独立だから①②の係数を比較して
\(\displaystyle\frac{1-k}{2}=\displaystyle\frac{1-h}{3}\)・・・③
\(\displaystyle\frac{1-k}{2}=h(1-t)\)・・・④
\(\displaystyle\frac{2}{3}k=ht\)・・・⑤
⑤を④に代入して
\(\displaystyle\frac{1-k}{2}=h-\displaystyle\frac{2}{3}k\)
よって
\(6h-k=3\)・・・⑥
③より
\(2h-3k=-1\)・・・⑦
⑥⑦より
\(k=\displaystyle\frac{3}{4}\), \(h=\displaystyle\frac{5}{8}\)
したがって⑤より
\(t=\displaystyle\frac{2}{3}\cdot\displaystyle\frac{k}{h}\)\(=\displaystyle\frac{4}{5}\) (\(0<t<1\)を満たす)
また、\(k=\displaystyle\frac{3}{4}\)を①に代入して
\(\overrightarrow{OX}=\displaystyle\frac{1-k}{2}\vec{a}+\displaystyle\frac{1-k}{2}\vec{b}+\displaystyle\frac{2}{3}k\vec{c}\)
\(=\displaystyle\frac{1}{8}\overrightarrow{OA}+\displaystyle\frac{1}{8}\overrightarrow{OB}+\displaystyle\frac{1}{2}\overrightarrow{OC}\)
(例題2)
四面体\(OABC\)において、\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(\overrightarrow{OC}=\vec{c}\) とおき、辺\(OA\)を\(1:2\)に内分する点を\(P\)、辺\(AB\)を\(2:1\)に内分する点を\(Q\)、辺\(BC\)を\(1:2\)に内分する点を\(R\)、辺\(OC\)を\(1:2\)に内分する点を\(S\)とする。
(1)図形\(PQRS\)が平行四辺形であることを示せ。
(2)線分\(PR\)と線分\(QS\)の交点を\(G\)とする。このとき、\(\vec{a},\vec{b},\vec{c}\)を用いて\(\overrightarrow{OG}\)を表せ。
(3)辺\(AC\)を\(1:1\)に内分する点を\(T\)、辺\(OB\)を\(1:1\)に内分する点を\(U\)、線分\(TU\)を\(2:1\)に内分する点を\(V\)とする。\(\vec{a},\vec{b},\vec{c}\) を用いて\(\overrightarrow{OV}\)を表し、点\(G\)と点\(V\)は一致することを示せ。
(解答)
(1)
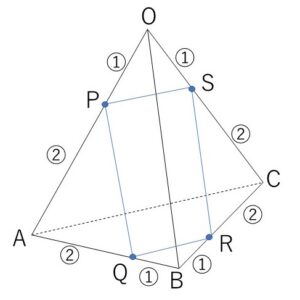
\(\overrightarrow{OP}=\displaystyle\frac{1}{3}\vec{a}\)
\(\overrightarrow{OQ}=\displaystyle\frac{\vec{a}+2\vec{b}}{3}\)
\(\overrightarrow{OR}=\displaystyle\frac{2\vec{b}+\vec{c}}{3}\)
\(\overrightarrow{OS}=\displaystyle\frac{1}{3}\vec{c}\)
よって
\(\overrightarrow{PS}=\overrightarrow{OS}-\overrightarrow{OP}\)
\(=\displaystyle\frac{1}{3}\vec{c}-\displaystyle\frac{1}{3}\vec{a}\)
\(\overrightarrow{QR}=\overrightarrow{OR}-\overrightarrow{OQ}\)
\(=\displaystyle\frac{1}{3}\vec{c}-\displaystyle\frac{1}{3}\vec{a}\)
したがって
\(\overrightarrow{PS}=\overrightarrow{QR}\) より、図形\(PQRS\)は対辺が平行で等しい四角形になるので、平行四辺形である。
(2)
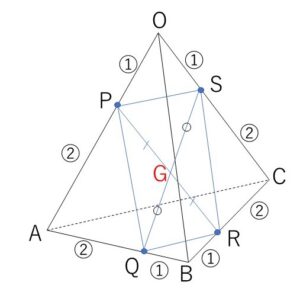
(1)より\(G\)は平行四辺形の対角線の交点になるから、線分\(PR\)の中点である。(\(QS\)の中点としてもよい)
よって
\(\overrightarrow{OG}=\displaystyle\frac{\overrightarrow{OP}+\overrightarrow{OR}}{2}\)
\(=\displaystyle\frac{1}{2}(\displaystyle\frac{1}{3}\vec{a}+\displaystyle\frac{2\vec{b}+\vec{c}}{3})\)
\(=\displaystyle\frac{1}{6}\vec{a}+\displaystyle\frac{1}{3}\vec{b}+\displaystyle\frac{1}{6}\vec{c}\)
(3)
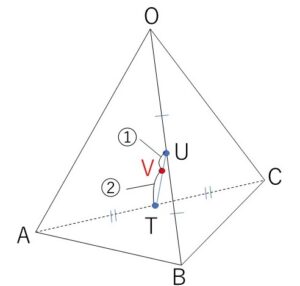
\(\overrightarrow{OT}=\displaystyle\frac{\vec{a}+\vec{c}}{2}\)
\(\overrightarrow{OU}=\displaystyle\frac{\vec{b}}{2}\)
よって
\(\overrightarrow{OV}=\displaystyle\frac{\overrightarrow{OT}+2\overrightarrow{OU}}{2+1}\)
\(=\displaystyle\frac{1}{3}(\displaystyle\frac{\vec{a}+\vec{c}}{2}+2\cdot\displaystyle\frac{\vec{b}}{2})\)
\(=\displaystyle\frac{1}{6}\vec{a}+\displaystyle\frac{1}{3}\vec{b}+\displaystyle\frac{1}{6}\vec{c}\)
したがって(2)より
\(\overrightarrow{OG}=\overrightarrow{OV}\) だから
点\(G\)と点\(V\)は一致する。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→同一平面上にある条件① back→同一直線上にある条件