球面と直線・交点の個数

球面と直線の交点に関する問題について見ていきます。

球面と直線の位置関係は次の3パターンに分類できます。
①2つの共有点をもつ　②1つの共有点をもつ(接する)　③共有点をもたない
これは直線の方程式を\(t\)の媒介変数で表し、球面の方程式と連立すると\(t\)の2次方程式になることにも合致します。

(例題1)
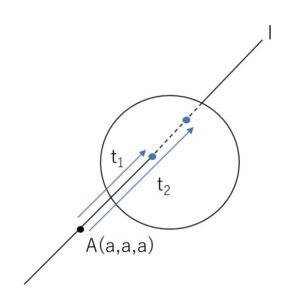
空間内に 点\(A(a,a,a)\) を通り、\(\vec{v}=(1,2,1)\) に平行な直線\(l\)と、点\(B(0,0,2)\) を中心とする半径\(2\)の球面\(S\)がある。球面\(S\)と直線\(l\)とが異なる2点で交わるような\(a\)の値の範囲を求めよ。

(解答)
直線\(l\)の方程式は実数\(t\)を用いて
\((x,y,z)=(a,a,a)+t(1,2,1)\)
\(=(a+t,a+2t,a+t)\)・・・①
と表せる。

また球面\(S\)の方程式は
\(x^2+y^2+(z-2)^2=4\)・・・②
である。

①を②に代入して
\((a+t)^2+(a+2t)^2+(a+t-2)^2=4\)
展開して\(t\)について整理すると
\(6t^2+2(4a-2)t+3a^2-4a=0\)・・・③

③は\(t\)の2次方程式で、\(a\)の値によって実数解\(t\)の個数が変わってきます。
\(t\)はもともと直線の方程式の媒介変数で、\(t\)の値によって直線上の点の位置が変わります。\(t\)が違う値ならば位置も変わるので、球面と直線が異なる2点で交わるときは③が異なる2つの実数解をもつことになります。
なお、1つの実数解(重解)をもつときは共有点は1個で(接している)、実数解をもたないときは、球面上かつ直線上にある点が存在しないことになるので共有点はなしです。

\(t\)の2次方程式
\(6t^2+2(4a-2)t+3a^2-4a=0\)・・・③
が異なる2つの実数解をもてば球面と直線は異なる2点で交わるから

\(\displaystyle\frac{D}{4}>0\)
\((4a-2)^2-6(3a^2-4a)>0\)
\(a^2-4a-2<0\)
したがって
\(2-\sqrt{6}<a<2+\sqrt{6}\)

(例題2)
空間に 球面\(S:x^2+y^2+z^2-4z=0\) と 定点\(A(0,1,4)\) がある。
(1)球面\(S\)の中心\(C\)の座標と半径を求めよ。
(2)直線\(AC\)と\(xy\)平面との交点\(P\)の座標を求めよ。
(3)\(xy\)平面上に点\(B(4,-1,0)\)をとるとき、直線\(AB\)と球面\(S\)の共有点の座標を求めよ。
(4)直線\(AQ\)と球面\(S\)が共有点をもつように点\(Q\)が\(xy\)平面上を動く。このとき、点\(Q\)の動く範囲を求めて、それを\(xy\)平面上に図示せよ。

(解答)
(1)
\(S:x^2+y^2+z^2-4z=0\) より
\(x^2+y^2+(z-2)^2=4\)

よって
中心\(C(0,0,2)\)、半径\(2\)

(2)

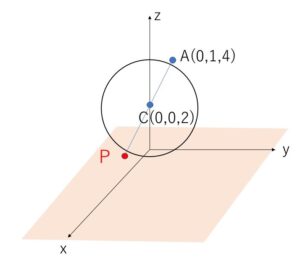
直線\(AC\)の方程式は\(t\)を実数として
\((x,y,z)=(0,1,4)+t(0,-1,-2)\)
\(=(0,1-t,4-2t)\)・・・①

\(AC\)上の点\(P\)は、\(xy\)平面上の点で\(z\)座標が\(0\)となるから
\(4-2t=0\)
\(t=2\)

よって①より
\(P(0,-1,0)\)

(3)

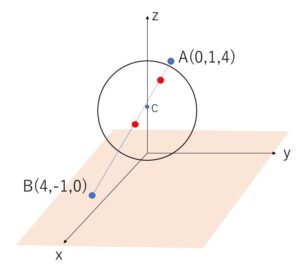
直線\(AB\)の方程式は、\(t\)を実数として
\((x,y,z)=(0,1,4)+t(4,-2,-4)\)
\(=(4t,1-2t,4-4t)\)・・・②

球面 \(x^2+y^2+z^2-4z=0\) に②を代入して
\((4t)^2+(1-2t)^2+(4-4t)^2-4(4-4t)=0\)
\(36t^2-20t+1=0\)
\((18t-1)(2t-1)=0\)
\(t=\displaystyle\frac{1}{18},\displaystyle\frac{1}{2}\)

よって②より球面との交点の座標は
\((\displaystyle\frac{2}{9},\displaystyle\frac{8}{9},\displaystyle\frac{34}{9})\), \((2,0,2)\)

(4)

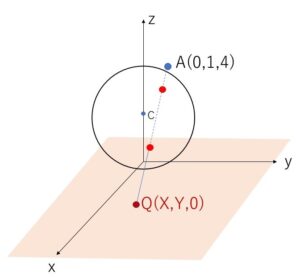
\(Q(X,Y,0)\) とおく。\(A(0,1,4)\) より直線\(AQ\)の方程式は

\((x,y,z)=(0,1,4)+t(X,Y-1,-4)\)
\(=(tX,1+t(Y-1),4-4t)\)・・・③

球面 \(x^2+y^2+z^2-4z=0\) に③を代入して

\((tX)^2+\{1+t(Y-1)\}^2+(4-4t)^2-4(4-4t)=0\)
\(t\)について整理すると
\(\{X^2+(Y-1)^2+16\}t^2+2(Y-9)t+1=0\)・・・④

\(X^2+(Y-1)^2+16≠0\) より④は\(t\)の2次方程式で、球面と共有点をもつとき④は実数解をもつから

\(\displaystyle\frac{D}{4}≧0\)
\((Y-9)^2-\{X^2+(Y-1)^2+16\}≧0\)

整理して、\(X→x\), \(Y→y\) におきかえると
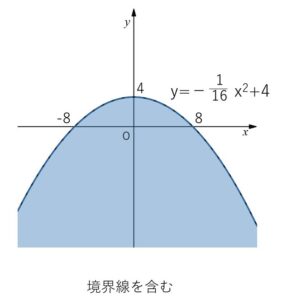
\(y≦-\displaystyle\frac{1}{16}x^2+4\)

したがって\(Q\)の動く範囲は図示すると次の通り。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→球面と平面　back→球面の方程式②