球面と平面の関係に関する例題について見ていきます。
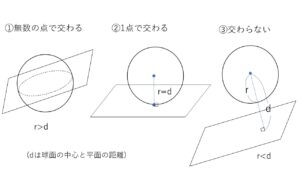
球面と平面の位置関係は次の3パターンに分類できます。
①共有点を無数にもつ(交線は円) ②共有点を1個もつ(接する) ③共有点をもたない
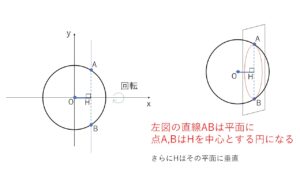
①について球面を平面で切断したときの切り口が円になるのは、球が円を回転してできる立体であることからわかります。
(例題1)
球面 \((x-1)^2+(y+3)^2+(z-2)^2=36\) と\(xy\)平面との交わりの円の、中心の座標と半径を求めよ。
(解答1)図形的に解く
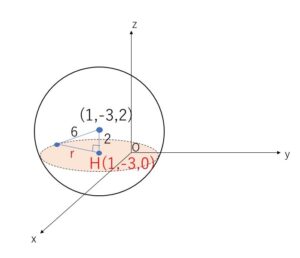
球面 \((x-1)^2+(y+3)^2+(z-2)^2=36\) の中心は \((1,-3,2)\) で、半径は\(6\)
球面の中心から\(xy\)平面に下ろした垂線の足を\(H\)とすると交わりの円の中心で、その座標は\(H(1,-3,0)\)
また円の半径\(r\)は
\(r=\sqrt{6^2-2^2}\)\(=4\sqrt{2}\)
(解答2)数式処理
\((x-1)^2+(y+3)^2+(z-2)^2=36\)・・・① かつ \(z=0\)・・・②
が球面と\(xy\)平面の交線(円)の方程式である。
②を①に代入した式を③とすると
①かつ② \(⇔\) ③かつ②
であり、③かつ②は
\((x-1)^2+(y+3)^2+(0-2)^2=36\) かつ \(z=0\)
よって交線の方程式は
\((x-1)^2+(y+3)^2=32\)・・・③ かつ \(z=0\)
③より
円の中心\((1,-3,0)\) 半径\(4\sqrt{2}\)
よって(例題2)のように交わる平面が傾いている場合には基本的には図形的に解く方法になります。
(例題2)
点\(O(0,0,0)\), 点\(A(9,0,0)\), 点\(B(0,\displaystyle\frac{9}{2},0)\), 点\(C(0,0,\displaystyle\frac{9}{2})\) とする。3点\(A,B,C\)を通る平面\(α\)と球面\(β:(x-4)^2+(y+3)^2+(z-1)^2=13\) について
(1)平面\(α\)の方程式を求めよ。
(2)平面\(α\)と球面\(β\)との交線である円\(S\)の中心\(D\)の座標を求めよ。
(3)点\(P\)が円\(S\)上を動くとき、\(OP^2\)の最大値と最小値を求めよ。
(解答)
(1)
平面\(α\)の方程式を
\(ax+by+cz+d=0\)
とする。
点\(A(9,0,0)\), 点\(B(0,\displaystyle\frac{9}{2},0)\), 点\(C(0,0,\displaystyle\frac{9}{2})\) を通るから
\(9a+d=0\)・・・①
\(\displaystyle\frac{9}{2}b+d=0\)・・・②
\(\displaystyle\frac{9}{2}c+d=0\)・・・③
よって \(a=-\displaystyle\frac{1}{9}d\), \(b=c=-\displaystyle\frac{2}{9}d\) となるから、平面の方程式は
\(-\displaystyle\frac{1}{9}dx-\displaystyle\frac{2}{9}dy-\displaystyle\frac{2}{9}dz+d=0\)・・・④
\(d=0\) とすると④は平面の方程式にならないので、\(d≠0\)。
したがって求める平面の方程式は
\(-\displaystyle\frac{1}{9}x-\displaystyle\frac{2}{9}y-\displaystyle\frac{2}{9}z+1=0\)
\(x+2y+2z-9=0\)
(2)
解答では最初に説明した内容とは少し違う観点で記述してみます。
(ちなみに(1)の平面の方程式を球面の方程式に代入すると複雑な式になるので却下です)
球面\(β:(x-4)^2+(y+3)^2+(z-1)^2=13\)
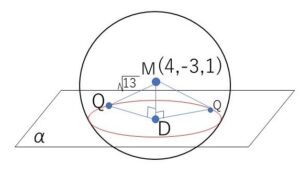
球面の中心を\(M(4,-3,1)\)とし、\(M\)から平面\(α\)に下した垂線の足を\(D\)とする。\(Q\)を交線である円上の点とすると
\(DQ^2=MQ^2-MD^2=13-MD^2\)
で、\(MD\)は\(M\)と平面\(α\)の距離だから一定の値になる。よって、\(DQ\)は一定の値で、\(D,Q\)のどちらも平面\(α\)上にあるので円の中心は\(D\)である。
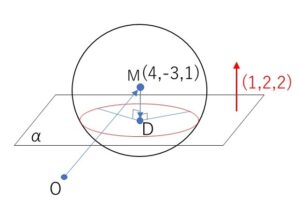
平面\(α\)の方程式は(1)より
\(x+2y+2z-9=0\)・・・⑤
この平面の法線ベクトルは\((1,2,2)\) だから
\(\overrightarrow{OD}=\overrightarrow{OM}+k(1,2,2)\)
\(=(4+k,-3+2k,1+2k)\)・・・⑥
\(D\)は平面\(α\)上の点だから⑥を⑤に代入して
\((4+k)+2(-3+2k)+2(1+2k)-9=0\)
\(k=1\)
⑥より
\(D(5,-1,3)\)
(3)
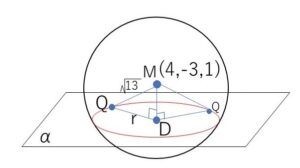
(2)より
\(\overrightarrow{MD}=k(1,2,2)=(1,2,2)\) だから
\(MD=\sqrt{9}\)
よって円\(S\)の半径\(r\)は
\(r=\sqrt{13-9}\)\(=2\)
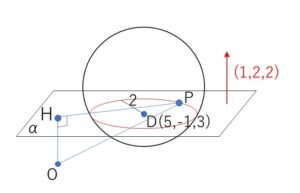
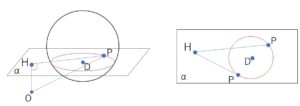
ここで、\(O\)から平面\(α\)に下した垂線の足を\(H\)とすると
\(\overrightarrow{OH}=s(1,2,2)\)
\(H\)は \(α:x+2y+2z-9=0\) 上にあるから
\(s+2\cdot2s+2\cdot2s-9=0\)
\(s=1\)
よって\(H(1,2,2)\)
また
\(OP^2=OH^2+HP^2=9+HP^2\)・・・⑦
より、\(OP^2\)の大小は、\(HP^2\)の大小と一致する。
そして、\(DH=\sqrt{4^2+(-3)^2+1^2}=\sqrt{26}>2\)
だから、\(H\)は円\(S\)の外側にある。
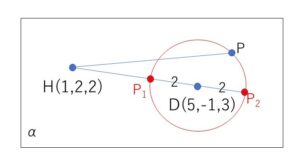
したがって、\(HP^2\)の
最小値は図の\(HP_1^2\)で
\(HP_1^2=(\sqrt{26}-2)^2=30-4\sqrt{26}\)
最大値は図の\(HP_2^2\)で
\(HP_2^2=(\sqrt{26}+2)^2=30+4\sqrt{26}\)
⑦より\(OP^2\)の
最小値は \(39-4\sqrt{26}\)
最大値は \(39+4\sqrt{26}\)
(例題3)
\(xyz\)空間において、3点 \(A(\sinθ,0,0)\), \(B(0,\cosθ,0)\), \(C(0,0,1)\) を通る平面\(α\)がある。ただし、\(0°<θ<90°\) とする。原点\(O(0,0,0)\) を中心とする球が平面\(α\)と接するとし、その接点を\(P\)とする。ベクトル\(\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}\) をそれぞれ\(\vec{a},\vec{b},\vec{c}\)とおくとき
(1)ベクトル\(\overrightarrow{OP}\)を\(\vec{a},\vec{b},\vec{c}\)を用いて表せ。
(2)ベクトル\(\overrightarrow{OP}\)の大きさを\(|\overrightarrow{OP}|\)とおくとき、\(|\overrightarrow{OP}|^2\)を\(θ\)を用いて表せ。
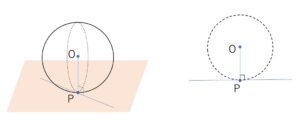
平面と球が接しているとき、中心\(O\)と接点\(P\)を通る直線\(OP\)は平面\(α\)に垂直です。中心\(O\)と接点\(P\)を通る平面(2点を通る平面なので無数にある)での断面を考えると、円と直線(平面の断面)が接していて、\(OP\)はこの直線と垂直です。どの断面でも同じことがいえるので、\(OP\)は平面\(α\)上の直線と垂直になるために、平面\(α\)と垂直です。
(解答)
(1)
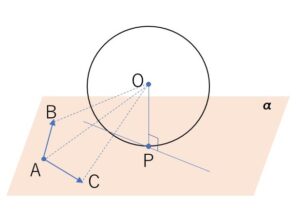
\(P\)は\(A,B,C\)を通る平面\(α\)上にあるので
\(\overrightarrow{OP}=r\vec{a}+s\vec{b}+t\vec{c}\)
\(r+s+t=1\)
とおける。また、\(OP\)は平面\(α\)と垂直だから、
\(\overrightarrow{OP} \perp \vec{AB}\), \(\overrightarrow{OP} \perp \vec{AC}\)
よって
\((r\vec{a}+s\vec{b}+t\vec{c})\cdot(\vec{b}-\vec{a})=0\)・・・①
\((r\vec{a}+s\vec{b}+t\vec{c})\cdot(\vec{c}-\vec{a})=0\)・・・②
\(A(\sinθ,0,0)\), \(B(0,\cosθ,0)\), \(C(0,0,1)\) より
\(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{c}=\vec{c}\cdot\vec{a}=0\)
\(|\vec{a}|^2=\sin^2θ\), \(|\vec{b}|^2=\cos^2θ\), \(|\vec{c}|^2=1\) なので①②は
\(s\cos^2θ-r\sin^2θ=0\)
\(t-r\sin^2θ=0\)
\(s=r\displaystyle\frac{\sin^2θ}{\cos^2θ}\)・・・③
\(t=r\sin^2θ\)・・・④
を \(r+s+t=1\)に代入して
\(r(1+\displaystyle\frac{\sin^2θ}{\cos^2θ}+\sin^2θ)=1\)
ゆえに
\(r=\displaystyle\frac{1}{1+\displaystyle\frac{\sin^2θ}{\cos^2θ}+\sin^2θ}\) (分母は\(0\)でない)
\(=\displaystyle\frac{\cos^2θ}{1+\sin^2θ\cos^2θ}\)
③④より
\(s=\displaystyle\frac{\sin^2θ}{1+\sin^2θ\cos^2θ}\), \(t=\displaystyle\frac{\sin^2θ\cos^2θ}{1+\sin^2θ\cos^2θ}\)
したがって
\(\overrightarrow{OP}=\displaystyle\frac{1}{1+\sin^2θ\cos^2θ}\{(\cos^2θ)\vec{a}+(\sin^2θ)\vec{b}+(\sin^2θ\cos^2θ)\vec{c}\}\)
(2)
(1)の結果から内積計算をしても、成分表示にして計算してもどちらもでよいです。
(1)より
\(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{c}=\vec{c}\cdot\vec{a}=0\)
\(|\vec{a}|^2=\sin^2θ\), \(|\vec{b}|^2=\cos^2θ\), \(|\vec{c}|^2=1\)
よって
\(|\overrightarrow{OP}|^2\)
\(=\left|\displaystyle\frac{1}{1+\sin^2θ\cos^2θ}\{(\cos^2θ)\vec{a}+(\sin^2θ)\vec{b}+(\sin^2θ\cos^2θ)\vec{c}\}\right|^2\)
\(=\left|\displaystyle\frac{1}{1+\sin^2θ\cos^2θ}\right|^2\left|\{(\cos^2θ)\vec{a}+(\sin^2θ)\vec{b}+(\sin^2θ\cos^2θ)\vec{c}\}\right|^2\)
\(=\displaystyle\frac{1}{(1+\sin^2θ\cos^2θ)^2}(\sin^2θ\cos^4θ+\sin^4θ\cos^2θ+\sin^4θ\cos^4θ)\)
\(=\displaystyle\frac{\sin^2θ\cos^2θ}{(1+\sin^2θ\cos^2θ)^2}(\cos^2θ+\sin^2θ+\sin^2θ\cos^2θ)\)
\(=\displaystyle\frac{\sin^2θ\cos^2θ}{(1+\sin^2θ\cos^2θ)^2}(1+\sin^2θ\cos^2θ)\)
\(=\displaystyle\frac{\sin^2θ\cos^2θ}{1+\sin^2θ\cos^2θ}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→球面と球面 back→球面と直線・交点の個数