空間ベクトルを利用する軌跡・領域の問題について見ていきます。
(例題1)
\(O\)を原点とする座標空間内に、4点 \(A(1,0,-1)\), \(B(2,1,0)\), \(C(-1,2,-1)\) \(D(-2,-1,3)\) がある。線分\(AB\)を \(s:(1-s)\) に内分する点を\(P\)とし、線分\(CD\)を \(t:(1-t)\) に内分する点を\(Q\)とする。
(1)\(\overrightarrow{OR}=\overrightarrow{PQ}\) で定まる点\(R\)に対し、\(\overrightarrow{OR}\)を\(s,t\)を用いて表せ。
(2)\(s,t\)が \(0≦s≦1\), \(0≦t≦1\) の範囲を動くとき、点\(R\)が描く図形\(F\)の面積を求めよ。
(3)点\(R\)が図形\(F\)上を動くとき、線分\(OR\)が動いてできる立体の体積を求めよ。
(解答)
(1)
\(A(1,0,-1)\), \(B(2,1,0)\)
線分\(AB\)を \(s:(1-s)\) に内分する\(P\)の座標は
\(P((1-s)+2s,s,-(1-s))\)\(=(s+1,s,s-1)\)
\(C(-1,2,-1)\) \(D(-2,-1,3)\)
線分\(CD\)を \(t:(1-t)\) に内分する点を\(Q\)の座標は
\(Q(-(1-t)-2t,2(1-t)-t,-(1-t)+3t)\)\(=(-t-1,-3t+2,4t-1)\)
よって
\(\overrightarrow{OR}\)\(=\overrightarrow{PQ}\)
\(=(-t-1,-3t+2,4t-1)-(s+1,s,s-1)\)
\(=(-s-t-2,-s-3t+2,-s+4t)\)
(2)
\(\overrightarrow{OR}\)
\(=(-s-t-2,-s-3t+2,-s+4t)\)
\(=(-2,2,0)+s(-1,-1,-1)+t(-1,-3,4)\)
\((-2,2,0)=\overrightarrow{ON}\)
\((-1,-1,-1)=\overrightarrow{NX}\)
\((-1,-3,4)=\overrightarrow{NY}\)
とおくと、
\(\overrightarrow{OR}=\overrightarrow{ON}+s\overrightarrow{NX}+t\overrightarrow{NY}\)
よって\(s,t\)が \(0≦s≦1\), \(0≦t≦1\) の範囲を動くとき、\(R\)は\(NX,NY\)を2辺とする平行四辺形の周および内部を移動する。
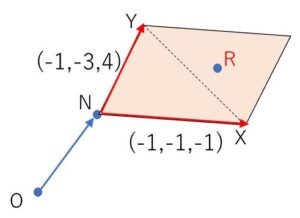
したがって\(R\)が描く図形\(F\)の面積\(S\)は、\(△NXY\)の面積を考えて
\(S=2×\displaystyle\frac{1}{2}\sqrt{(1+9+16)(1+1+1)-(1+3-4)^2}\)
\(=\sqrt{78}\)
(3)
線分\(OR\)が動いてできる立体は、図形\(F\)を底面、\(O\)を頂点とする四角錐である。
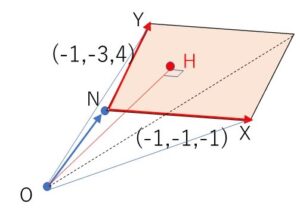
\(\overrightarrow{NX},\overrightarrow{NY}\)に垂直なベクトルを \(\vec{n}=(a,b,c)\) とすると
\(-a-b-c=0\), \(-a-3b+4c=0\)
よって
\(b=\displaystyle\frac{5}{2}c\), \(a=-\displaystyle\frac{7}{2}c\) となるから
\(\vec{n}=(-\displaystyle\frac{7}{2}c,\displaystyle\frac{5}{2}c,c)\)
\(c=2\)とすると、底面に垂直なベクトルの1つとして、\(\vec{n}=(-7,5,2)\) がとれる。
ゆえに\(O\)から底面を含む平面に下ろした垂線の足を\(H\)とすると
\(\overrightarrow{OH}=k(-7,5,2)\)・・・①
\(H\)は底面を含む平面上にあるので、(1)(2)より
\(\overrightarrow{OH}=(-s-t-2,-s-3t+2,-s+4t)\)・・・②
とも表せる。
①②より成分を比較して
\(-7k=-s-t-2\)
\(5k=-s-3t+2\)
\(2k=-s+4t\)
これらから\(k,s,t\) を求めると
\(k=\displaystyle\frac{4}{13}\), \(s=0\), \(t=\displaystyle\frac{2}{13}\)
①より
\(\overrightarrow{OH}=\displaystyle\frac{4}{13}(-7,5,2)\) だから
\(|\overrightarrow{OH}|=\displaystyle\frac{4}{13}\sqrt{49+25+4}\)\(=\displaystyle\frac{4\sqrt{78}}{13}\)
したがって四角錐の体積\(V\)は、(2)より底面積が\(\sqrt{78}\)だから
\(V=\displaystyle\frac{1}{3}\cdot\sqrt{78}\cdot\displaystyle\frac{4\sqrt{78}}{13}\)\(=8\)
(例題2)
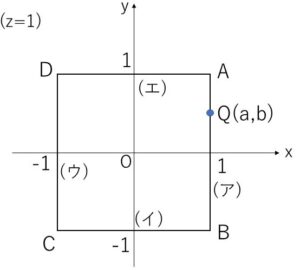
\(xyz\)空間内の平面 \(z=2\) 上に点\(P\)があり、平面 \(z=1\) 上に点\(Q\)がある。直線\(PQ\)と\(xy\)平面の交点を\(R\)とする。
(1)\(P(0,0,2)\)とする。点\(Q\)が平面\(z=1\)上で点\((0,0,1)\)を中心とする半径\(1\)の円周上を動くとき、点\(R\)の軌跡の方程式を求めよ。
(2)平面\(z=1\)上に 4点\(A(1,1,1)\), \(B(1,-1,1)\), \(C(-1,-1,1)\), \(D(-1,1,1)\) をとる。点\(P\)が平面\(z=2\)上で点\((0,0,2)\)を中心とする半径\(1\)の円周上を動き、点\(Q\)が正方形\(ABCD\)の周上を動くとき、点\(R\)が動きうる領域を\(xy\)平面上に図示し、その面積を求めよ。
(解答)
(1)
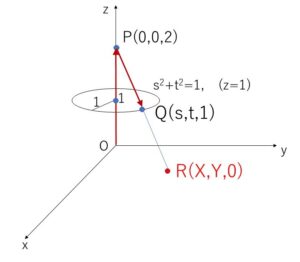
\(R(X,Y,0)\), \(Q(s,t,1)\) とおくと、\(Q\)は円周上の点だから
\(s^2+t^2=1\)・・・①
\(P,Q,R\)は一直線上にあるから、\(P(0,0,2)\) より
\(\overrightarrow{OQ}=\overrightarrow{OP}+k\overrightarrow{PR}\)
\(=(0,0,2)+k(X,Y,-2)\)
\(=(kX,kY,2-2k)\)・・・②
\(\overrightarrow{OQ}=(s,t,1)\) より
\(s=kX\)・・・③
\(t=kY\)・・・④
\(1=2-2k\)・・・⑤
⑤より \(k=\displaystyle\frac{1}{2}\)
よって③④より
\(s=\displaystyle\frac{1}{2}X\), \(t=\displaystyle\frac{1}{2}Y\)
これらを①に代入すると
\((\displaystyle\frac{1}{2}X)^2+(\displaystyle\frac{1}{2}Y)^2=1\)
\(R(X,Y,0)\)であり、\(X→x\), \(Y→y\) として整理すると、\(R\)の軌跡の方程式は
\(x^2+y^2=4\), \(z=0\)
(2)
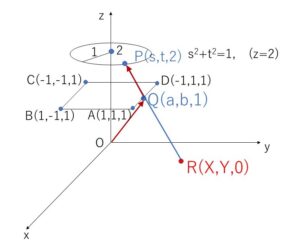
\(R(X,Y,0)\), \(Q(a,b,1)\), \(P(s,t,2)\) とおく。
\(P\)は円周上にあるので
\(s^2+t^2=1\)・・・⑥
\(P,Q,R\)は一直線上にあるから
\(\overrightarrow{OP}=\overrightarrow{OQ}+k\overrightarrow{QR}\)
\(=(a,b,1)+k(X-a,Y-b,-1)\)
\(=(a+k(X-a),b+k(Y-b),1-k)\)
\(\overrightarrow{OP}=(s,t,2)\) より
\(s=a+k(X-a)\)・・・⑦
\(t=b+k(Y-b)\)・・・⑧
\(2=1-k\)・・・⑨
⑨より \(k=-1\)
⑦⑧より
\(s=-X+2a\), \(t=-Y+2b\)
これらを⑥に代入して
\((-X+2a)^2+(-Y+2b)^2=1\)
\(R(X,Y,0)\)であり、\(X→x\), \(Y→y\) とすると、\(R\)に関する方程式は
\((x-2a)^2+(y-2b)^2=1\)・・・⑩ \(z=0\)
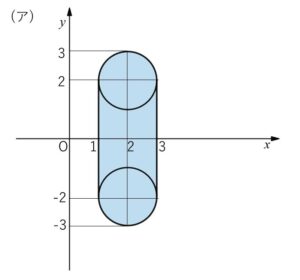
(ア)\(Q\)が辺\(AB\)上にあるとき
\(a=1\), \(-1≦b≦1\) だから⑩は
\((x-2)^2+(y-2b)^2=1\) (\(-2≦2b≦2\))
円の中心は \((2,2b)\)、半径は\(1\)だから、\(R\)の動く領域は次の通り。
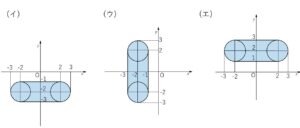
同様に\(Q\)が
(イ)辺\(BC\)上にあるとき (ウ)辺\(CD\)上にあるとき (エ)辺\(DA\)上にあるとき
の\(R\)の動く領域は次の通り。
したがって(ア)~(エ)をまとめると、\(R\)の動く領域は次の通り。
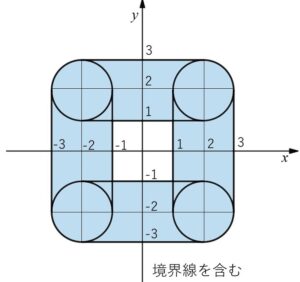
領域の面積は
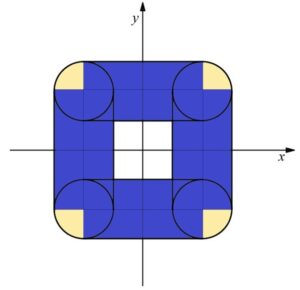
\((4×4)-(2×2)+(1×4)×4+π×1^2\)
\(=28+π\)
(面積計算は下図を参考にしてください)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間ベクトルの終点の存在範囲 back→空間図形の証明問題