ベクトルを利用した空間図形の証明問題について見ていきます。
(例題1)
四面体\(ABCD\)の3辺\(AB,BC,CD\)上に、それぞれ、頂点とは異なる点\(P,Q,R\)をとり、三角形\(PQR\)の重心を\(G\)、三角形\(BCD\)の重心を\(H\)とする。3点\(A,G,H\)が同一直線上にあるとき
\(\displaystyle\frac{2}{3}<\displaystyle\frac{AG}{AH}<1\)
であることを示せ。
(解答)
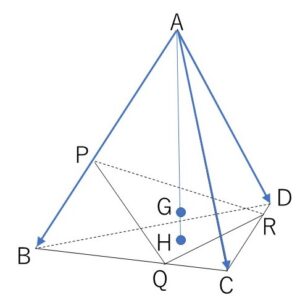
\(\overrightarrow{AB}=\vec{b}\), \(\overrightarrow{AC}=\vec{c}\), \(\overrightarrow{AD}=\vec{d}\) とおく。
\(\overrightarrow{AP}=p\vec{b}\) (\(0<p<1\))
\(\overrightarrow{AQ}=(1-q)\vec{b}+q\vec{c}\) (\(0<q<1\))
\(\overrightarrow{AR}=(1-r)\vec{c}+r\vec{d}\) (\(0<r<1\))
と表せ、
\(\overrightarrow{AG}=\displaystyle\frac{1}{3}(\overrightarrow{AP}+\overrightarrow{AQ}+\overrightarrow{AR})\)
\(=\displaystyle\frac{1}{3}(p+1-q)\vec{b}+\displaystyle\frac{1}{3}(q+1-r)\vec{c}+\displaystyle\frac{1}{3}r\vec{d}\)・・・①
\(\overrightarrow{AH}=\displaystyle\frac{1}{3}(\vec{b}+\vec{c}+\vec{d})\)
また\(A,G,H\)が一直線上にあるので、実数\(k\)を用いて
\(\overrightarrow{AG}=k\overrightarrow{AH}\)
\(=\displaystyle\frac{1}{3}k(\vec{b}+\vec{c}+\vec{d})\)・・・②
\(\vec{b},\vec{c},\vec{d}\) は一次独立だから①②の係数を比較すると
\(p+1-q=k\)・・・③
\(q+1-r=k\)・・・④
\(r=k\)・・・⑤
④⑤より
\(q=2k-1\)
③より
\(p=3k-2\)
\(0<p<1\), \(0<q<1\), \(0<r<1\) に代入すると
\(0<3k-2<1\), \(0<2k-1<1\), \(0<k<1\)
よって
\(\displaystyle\frac{2}{3}<k<1\), \(\displaystyle\frac{1}{2}<k<1\), \(0<k<1\) より、共通部分は
\(\displaystyle\frac{2}{3}<k<1\)
\(\overrightarrow{AG}=k\overrightarrow{AH}\) より
\(k=\displaystyle\frac{|\overrightarrow{AG}|}{|\overrightarrow{AH}|}\) だから
\(\displaystyle\frac{2}{3}<\displaystyle\frac{AG}{AH}<1\)
(例題2)
四面体\(OABC\)は次の2つの条件
(i)\(OA \perp BC\), \(OB \perp AC\), \(OC \perp AB\)
(ii)4つの面の面積がすべて等しい
を満たしている。このとき、この四面体は正四面体であることを示せ。
(解答)
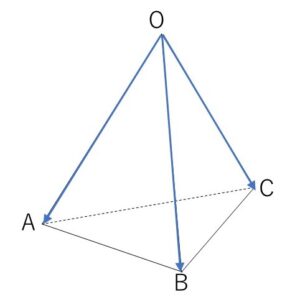
\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(\overrightarrow{OC}=\vec{c}\) とおく。
(i)\(OA \perp BC\), \(OB \perp AC\), \(OC \perp AB\) より
\(\vec{a}\cdot(\vec{c}-\vec{b})=0\)
\(\vec{b}\cdot(\vec{c}-\vec{a})=0\)
\(\vec{c}\cdot(\vec{b}-\vec{a})=0\)
よって
\(\vec{a}\cdot\vec{b}=\vec{c}\cdot\vec{a}\), \(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{c}\), \(\vec{b}\cdot\vec{c}=\vec{c}\cdot\vec{a}\) となるから
\(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{c}=\vec{c}\cdot\vec{a}\)・・・①
また条件(ii)より
\(△OAB=△OBC=△OCA\) だから
\(\displaystyle\frac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}=\displaystyle\frac{1}{2}\sqrt{|\vec{b}|^2|\vec{c}|^2-(\vec{b}\cdot\vec{c})^2}=\displaystyle\frac{1}{2}\sqrt{|\vec{c}|^2|\vec{a}|^2-(\vec{c}\cdot\vec{a})^2}\)
よって
\(|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2=|\vec{b}|^2|\vec{c}|^2-(\vec{b}\cdot\vec{c})^2=|\vec{c}|^2|\vec{a}|^2-(\vec{c}\cdot\vec{a})^2\)
①より
\(|\vec{a}|^2|\vec{b}|^2=|\vec{b}|^2|\vec{c}|^2=|\vec{c}|^2|\vec{a}|^2\)
左辺と中辺から、\(|\vec{a}|=|\vec{c}|\)
中辺と右辺から、\(|\vec{a}|=|\vec{b}|\)
したがって
\(|\vec{a}|=|\vec{b}|=|\vec{c}|\)
\(OA=OB=OC\)・・・(ア)
条件(i)が交わらない2辺の組になっていて、条件(ii)も4面全部についての条件
なので、\(A\)を始点とするベクトルとしても同じことが言えるはずです(対称性がある)。
すると、\(AO=AB=AC\) が示せますが、まだ\(BC\)については等しいことがいえないので、さらに\(B\)を始点とするベクトルで同じ検討をします。(\(C\)始点は過剰になる)
解答では同様にくらいの表現と良いと思います。
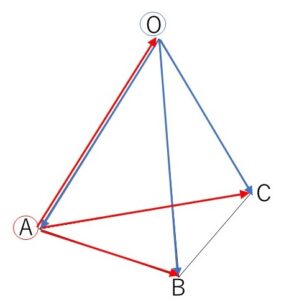
\(A\)を始点とするベクトルで同様に検討すると
\(AO=AB=AC\)・・・(イ)
\(B\)を始点とするベクトルについては
\(BO=BA=BC\)・・・(ウ)
がそれぞれ得られる。
(ア)(イ)(ウ)より
\(OA=OB=OC=AB=AC=BC\)
したがって四面体\(OABC\)の6辺の長さは等しいので、正四面体になる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間ベクトルによる軌跡・領域(投影) back→球面と球面