平面の方程式について見ていきます。
まずは簡単な座標軸に垂直な平面から始めていきます。
・座標軸に垂直な平面(\(xy,yz,zx\)平面に平行な平面)
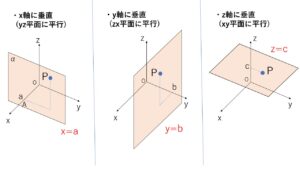
点\(P(a,b,c)\)を通り、\(x\)軸に垂直な平面を\(α\)とすると、\(α\)と\(x\)軸との交点\(A\)の座標は \((a,0,0)\) です。平面\(α\)は\(x\)座標が常に\(a\)で、\(y,z\)座標は任意である点の集合なので、平面\(α\)の方程式は \(x=a\) となります。同様に\(P\)を通り\(y\)軸,\(z\)軸に垂直な平面の方程式は、それぞれ \(y=b\), \(z=c\) となります。
とくに \(a=0\) とすると、「\(x=0\) は \(yz\)平面」を表し、
同様に、「\(y=0\) は \(zx\)平面」、「\(z=0\) は \(xy\)平面」を表します。
また図より、\(x=a\) は \(x=0\) つまり \(yz\)平面に平行であり、
同様に、\(y=b\) は \(zx\)平面に平行、\(z=c\) は \(xy\)平面に平行となります。
(ア)同一平面上にある条件を利用する (イ)法線ベクトルを利用する
(ア)はお馴染みの内容で、(イ)に関してはこれを発展させると平面の方程式の一般形を導くことができます。
・平面の方程式(同一平面上にある条件)
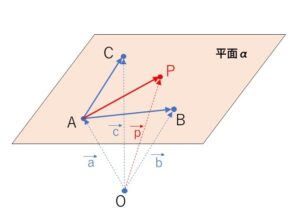
\(A(\vec{a}),B(\vec{b}),C(\vec{c})\) を同一直線上にない3点とするとき、\(r,s,t\)を実数として、\(A,B,C\)を通る平面上の点\(P(\vec{p})\)について
\(\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}\)
\(⇔\) \(\vec{p}=r\vec{a}+s\vec{b}+t\vec{c}\) (\(r+s+t=1\))
(解説)
同じ直線上にない3点 \(A(\vec{a})\), \(B(\vec{b})\), \(C(\vec{c})\) を通る平面を\(α\)とします。(\(A,B,C\)が同一直線上にあると平面が1つに定まらない)
点\(P(\vec{p})\)が\(α\)上にあるとき、実数\(s,t\)を用いて\(\overrightarrow{AP}\)を次のように表すことができます。
\(\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}\)・・・①
(\(A,B,C\)が一直線上にないためにこの形で表せます。)
よって
\(\vec{p}-\vec{a}=s(\vec{b}-\vec{a})+t(\vec{c}-\vec{a})\)
\(\vec{p}=(1-s-t)\vec{a}+s\vec{b}+t\vec{c}\)
ここで、係数の和が \((1-s-t)+s+t=1\) になることに着目して
\(1-s-t=r\) とおくと\(r\)も実数であり
\(\vec{p}=r\vec{a}+s\vec{b}+t\vec{c}\) (\(r+s+t=1\))・・・②
また、②のベクトルの等式について位置ベクトルの基準を\(O\)とすると次のように表されます。
\(\overrightarrow{OP}=r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}\) (\(r+s+t=1\))
・平面の方程式(法線ベクトル)
平面に垂直な直線は、平面に含まれるどの直線にも垂直であることを利用して、平面の方程式を求めることもできます。
点\(A(\vec{a})\)を通り、\(\vec{0}\)でない\(\vec{n}\)に垂直な平面上の点を\(P(\vec{p})\)とすると
\(\vec{n}\cdot(\vec{p}-\vec{a})=0\)
(解説)
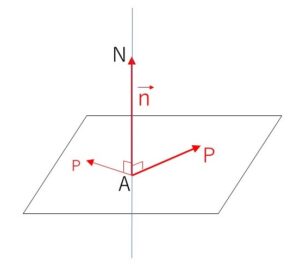
\(\vec{n}\)は、平面に含まれる任意の直線に垂直なので
\(\overrightarrow{AP} \perp \vec{n}\) または \(\overrightarrow{AP}=\vec{0}\) (\(P\)が\(A\)に一致)
よって
\(\vec{n}\cdot\overrightarrow{AP}=0\)
したがって
\(\vec{n}\cdot(\vec{p}-\vec{a})=0\)・・・③
また、\(\vec{n}\)のように平面に垂直なベクトルを法線ベクトル、図の直線\(AN\)のような平面に垂直な直線を法線とよびます。
さらに、\(P(x,y,z)\), \(A(x_0,y_0,z_0)\)、法線ベクトルを \(\vec{n}=(a,b,c)\) とすると③より
\((a,b,c)\cdot(x-x_0,y-y_0,z-z_0)=0\)
よって
\(a(x-x_0)+b(y-y_0)+c(z-z_0)=0\)・・・④ (点\(A\)を通る平面の方程式)
さらに展開して 定数項を \(-ax_0-by_0-cz_0=d\) とおくと
\(ax+by+cz+d=0\)・・・⑤ (平面の方程式の一般形)
となります。すると\(x,y,z\)の1次方程式が平面を表し、④や⑤の形で表された平面の法線ベクトルの1つが係数をとった \((a,b,c)\) となっていることが分かります。
(例題1)
直線 \(l:\displaystyle\frac{x+1}{2}=\displaystyle\frac{y-1}{3}=\displaystyle\frac{z-1}{4}\) に垂直で、点\(A(2,2,2)\) を通る平面\(α\)の方程式を求めよ。
(解答)
平面\(α\)の法線ベクトルの1つが、直線\(l\)の方向ベクトル\((2,3,4)\)であり、平面\(α\)が点\(A(2,2,2)\)を通るから
\(2(x-2)+3(y-2)+4(z-2)=0\)
整理して
\(2x+3y+4z-18=0\)
(注)
直線の方程式の分母の数字をとったものが、直線の方向ベクトルとなることを知っていれば一瞬ですが、知らない場合には次のように考えます。
\(l:\displaystyle\frac{x+1}{2}=\displaystyle\frac{y-1}{3}=\displaystyle\frac{z-1}{4}=t\) とおいて
\(x+1=2t\)
\(y-1=3t\)
\(z-1=4t\) より
\(x=-1+2t\)
\(y=1+3t\)
\(z=1+4t\)
ベクトル表示にすると
\((x,y,z)=(-1,1,1)+t(2,3,4)\)
すると直線の方向ベクトルが\((2,3,4)\)となることが分かります。
(例題2)
3点 \(A(0,1,2)\), \(B(1,2,1)\), \(C(4,-1,2)\) を通る平面\(α\)の方程式を求めよ。
なお一直線上にない3点を通る平面はただ1通りに決定します。
(解答1)法線ベクトルを求める方法
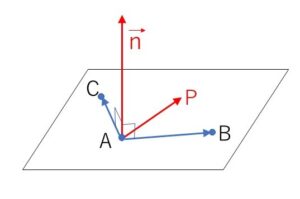
\(A(0,1,2)\), \(B(1,2,1)\), \(C(4,-1,2)\) より
\(\overrightarrow{AB}=(1,1,-1)\), \(\overrightarrow{AC}=(4,-2,0)\)
平面の法線ベクトルを \(\vec{n}=(a,b,c)\) とおくと
\(\vec{n}\cdot\overrightarrow{AB}=0\), \(\vec{n}\cdot\overrightarrow{AC}=0\)
\(a+b-c=0\)・・・① \(4a-2b=0\)・・・②
①②より \(b=2a\), \(c=3a\)
よって、\(\vec{n}=(a,2a,3a)\) であり\(a=1\)とすれば法線ベクトルの1つは
\(\vec{n}=(1,2,3)\)
平面\(α\)は\(A(0,1,2)\) を通るから (\(B\) or \(C\) でもよい)、平面の方程式は
\(1\cdot(x-0)+2(y-1)+3(z-2)=0\)
したがって
\(x+2y+3z-8=0\)
(解答2)平面の方程式の一般形に代入する方法
平面\(α\)の方程式を
\(ax+by+cz+d=0\) とおく。
\(A(0,1,2)\), \(B(1,2,1)\), \(C(4,-1,2)\) を通るから
\(0+b+2c+d=0\)・・・③
\(a+2b+c+d=0\)・・・④
\(4a-b+2c+d=0\)・・・⑤
⑤-③より
\(4a-2b=0\)
よって \(b=2a\)
④-③より
\(a+b-c=0\)
よって \(c=3a\)
③より \(d=-8a\)
したがって平面の方程式は
\(ax+2ay+3az-8a=0\)
\(a=0\) とすると平面を表さないので、\(a≠0\)
ゆえに、求める方程式は
\(x+2y+3z-8=0\)
(解答3)同一平面上にある条件を利用する方法
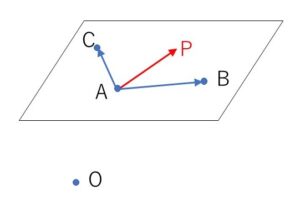
平面\(α\)上の点を\(P(x,y,z)\)とすると、実数\(s,t\)を用いて
\(\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}\)
\(A(0,1,2)\), \(B(1,2,1)\), \(C(4,-1,2)\) より
\(\overrightarrow{AB}=(1,1,-1)\), \(\overrightarrow{AC}=(4,-2,0)\), \(\overrightarrow{AP}=(x,y-1,z-2)\) だから
\((x,y-1,z-2)=s(1,1,-1)+t(4,-2,0)\)
成分を比較して
\(x=s+4t\)・・・⑥
\(y-1=s-2t\)・・・⑦
\(z-2=-s\)・・・⑧
⑧を⑥⑦に代入して
\(x=-z+2+4t\)・・・⑨
\(y-1=-z+2-2t\)・・・⑩
⑩から \(4t=-2y-2z+6\)
これを⑨に代入して
\(x=-z+2-2y-2z+6\)
整理して
\(x+2y+3z-8=0\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→直線と平面の交点、直線と平面の平行 back→点と直線の距離、直線と直線の距離