直線と平面の交点、直線と平面の平行

直線と平面の関係についての例題です。

(例題1)
(1)2点 \(A(3,-1,2)\), \(B(5,1,1)\) を通る直線と、\(xy\)平面との交点\(P\)の座標を求めよ。
(2)直線 \((x,y,z)=(-1,1,1)+t(1,3,-2)\) と 平面 \(2x-y+3z=3\) の交点の座標を求めよ。

(解答)
(1)

\(A,B\)を通る直線は \(\overrightarrow{AB}=(2,2,-1)\) より
\((x,y,z)=(3,-1,2)+s(2,2,-1)\)
と表せる。

よって
\(x=3+2s\)・・・①
\(y=-1+2s\)・・・②
\(z=2-s\)・・・③

\(xy\)平面上では\(z=0\)だから
\(2-s=0\)
ゆえに \(s=2\)

①②より交点の座標は
\((7,3,0)\)

(2)

直線の方程式より \((x,y,z)=(-1+t,1+3t,1-2t)\)
\(x=-1+t\),　\(y=1+3t\),　\(x=1-2t\)・・・(※)

直線上の点が、平面 \(2x-y+3z=3\)・・・④ 上にあるから
(※)の3式を④に代入して

\(2(-1+t)-(1+3t)+3(1-2t)=3\)
よって \(t=-\displaystyle\frac{3}{7}\)

(※)より交点の座標は
\((-\displaystyle\frac{10}{7},-\displaystyle\frac{2}{7},\displaystyle\frac{13}{7})\)

(例題2)
空間に直線
\(l:(x,y,z)=(0,-3,-2)+t(1,3,2)\) (\(t\)はパラメーター)
および点\(P(1,2,1)\)がある。直線\(l\)を含み、点\(P\)を通る平面\(α\)と\(z\)軸との交点の座標を求めよ。

(解答)

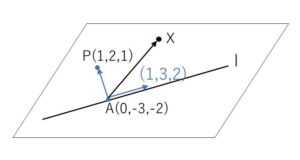
直線\(l\)の点\((0,-3,-2)\)を\(A\)、方向ベクトルを \(\vec{u}=(1,3,2)\) とおくと、平面\(α\)上の点\(X\)について

\(\overrightarrow{AX}=s\vec{u}+t\overrightarrow{AP}\)

が成り立つ。\(X(x,y,z)\) とおくと、
\((x,y+3,z+2)=s(1,3,2)+t(1,5,3)\)

成分を比較して
\(x=s+t\)・・・①
\(y+3=3s+5t\)・・・②
\(z+2=2s+3t\)・・・③

\(X\)が\(z\)軸上の点であるとき \(x=y=0\) だから①②より
\(0=s+t\), 　\(3=3s+5t\)
これより \(s=-\displaystyle\frac{3}{2}\), \(t=\displaystyle\frac{3}{2}\)

したがって③より求める\(z\)軸上の交点の座標は
\((0,0,-\displaystyle\frac{1}{2})\)

(例題3)
四面体\(OABC\)の辺\(OA,OB\)上にそれぞれ点\(D,E\)をとる。ただし点\(D\)は、点\(A,O\)と異なり、\(AE\)と\(BD\)の交点\(F\)は線分\(AE,BD\)をそれぞれ \(2:1\), \(3:1\) の比に内分している。また、辺\(BC\)を \(t:1\) (\(t>0\)) の比に内分する点\(P\)をとり、\(CE\)と\(OP\)の交点を\(Q\)とする。

(1)\(\overrightarrow{OF}\)を\(\overrightarrow{OA}\)と\(\overrightarrow{OB}\)を用いて表せ。
(2)\(\overrightarrow{OQ}\)を\(\overrightarrow{OB},\overrightarrow{OC}\)および\(t\)を用いて表せ。
(3)直線\(FQ\)と平面\(ABC\)が平行になるような\(t\)の値を求めよ。

(解答)
(1)
(\(\overrightarrow{OF}\)を2通りに表す)

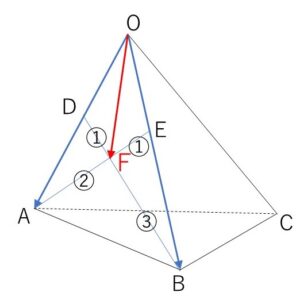
\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\) とおく。

\(\overrightarrow{OD}=k\vec{a}\)と表せるので

\(\overrightarrow{OF}=\displaystyle\frac{3\overrightarrow{OD}+\vec{b}}{1+3}\)\(=\displaystyle\frac{3}{4}k\vec{a}+\displaystyle\frac{1}{4}\vec{b}\)・・・①

また、\(\overrightarrow{OE}=l\vec{b}\) と表せるので

\(\overrightarrow{OF}=\displaystyle\frac{\vec{a}+2\overrightarrow{OE}}{2+1}\)\(=\displaystyle\frac{1}{3}\vec{a}+\displaystyle\frac{2}{3}l\vec{b}\)・・・②

\(\vec{a},\vec{b}\)は\(\vec{0}\)でなく、平行ではないので①②より係数を比較して

\(\displaystyle\frac{3}{4}k=\displaystyle\frac{1}{3}\),　\(\displaystyle\frac{1}{4}=\displaystyle\frac{2}{3}l\)

よって
\(k=\displaystyle\frac{4}{9}\),  \(l=\displaystyle\frac{3}{8}\)
(このとき\(D,E\)は辺上の点であり、題意を満たす)

したがって①より
\(\overrightarrow{OF}=\displaystyle\frac{1}{3}\overrightarrow{OA}+\displaystyle\frac{1}{4}\overrightarrow{OB}\)

(2)

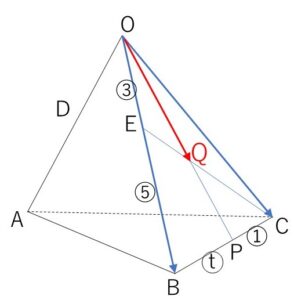
\(\overrightarrow{OC}=\vec{c}\) とおくと

\(Q\)は\(OP\)上の点だから
\(\overrightarrow{OQ}=u\overrightarrow{OP}=\displaystyle\frac{u\vec{b}+ut\vec{c}}{t+1}\)・・・③

(1)より\(\overrightarrow{OE}=\displaystyle\frac{3}{8}\vec{b}\) だから

\(\overrightarrow{OQ}=\displaystyle\frac{u}{t+1}\vec{b}+\displaystyle\frac{ut}{t+1}\vec{c}\)

\(=\displaystyle\frac{u}{t+1}\cdot\displaystyle\frac{8}{3}\overrightarrow{OE}+\displaystyle\frac{ut}{t+1}\vec{c}\)

\(Q\)は\(EC\)上の点でもあるから
\(\displaystyle\frac{u}{t+1}\cdot\displaystyle\frac{8}{3}+\displaystyle\frac{ut}{t+1}=1\)

(\(t\)は与えられた文字で、\(u\)は勝手においた文字なので\(u\)を求めると)

両辺に\(3(t+1)\)を掛けて
\(8u+3ut=3(t+1)\)
\(u(8+3t)=3(t+1)\)
よって
\(u=\displaystyle\frac{3(t+1)}{3t+8}\)

したがって③より
\(\overrightarrow{OQ}=u\cdot\displaystyle\frac{1}{t+1}\vec{b}+u\cdot\displaystyle\frac{t}{t+1}\vec{c}\)

\(=\displaystyle\frac{3}{3t+8}\overrightarrow{OB}+\displaystyle\frac{3t}{3t+8}\overrightarrow{OC}\)

(3)

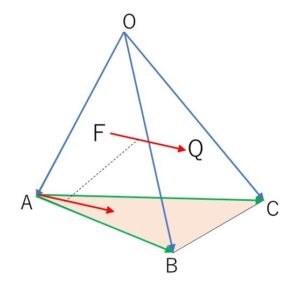
直線\(FQ\)と平面\(ABC\)が平行であるとき
\(\overrightarrow{FQ}=x\overrightarrow{AB}+y\overrightarrow{AC}\) と表せる。

よって
\(\overrightarrow{FQ}=x(\vec{b}-\vec{a})+y(\vec{c}-\vec{a})\)

\(=-(x+y)\vec{a}+x\vec{b}+y\vec{c}\)・・・④

また(1)(2)より
\(\overrightarrow{FQ}=\overrightarrow{OQ}-\overrightarrow{OF}\)

\(=\displaystyle\frac{3}{3t+8}\vec{b}+\displaystyle\frac{3t}{3t+8}\vec{c}-(\displaystyle\frac{1}{3}\vec{a}+\displaystyle\frac{1}{4}\vec{b})\)

\(=-\displaystyle\frac{1}{3}\vec{a}+(\displaystyle\frac{3}{3t+8}-\displaystyle\frac{1}{4})\vec{b}+\displaystyle\frac{3t}{3t+8}\vec{c}\)・・・⑤

\(\vec{a},\vec{b},\vec{c}\)は同一平面上にないので④⑤の係数を比較して

\(-(x+y)=-\displaystyle\frac{1}{3}\)・・・⑥

\(x=\displaystyle\frac{3}{3t+8}-\displaystyle\frac{1}{4}\)・・・⑦

\(y=\displaystyle\frac{3t}{3t+8}\)・・・⑧

⑦⑧を⑥に代入して
\(\displaystyle\frac{3}{3t+8}-\displaystyle\frac{1}{4}+\displaystyle\frac{3t}{3t+8}=\displaystyle\frac{1}{3}\)

\(\displaystyle\frac{3t+3}{3t+8}=\displaystyle\frac{7}{12}\)

\(12(3t+3)=7(3t+8)\)

よって \(t=\displaystyle\frac{4}{3}\)
(このとき⑦⑧より\(x,y\)は実数となる)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→平面に下ろした垂線①　back→平面の方程式