引き続き平面の垂線に関する例題です。
(例題1)
点\(A(x_0,y_0,z_0)\) と 平面 \(ax+by+cz+d=0\) の距離\(d\)は次の式で与えられることを示せ。なお、点\(A\)から平面に下ろした垂線を\(AH\)とするとき、線分\(AH\)の長さを点\(A\)と平面の距離という。
\(d=\displaystyle\frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}\)
なお平面上の点と点\(A\)を結ぶ線分のうち、もっとも短いものが距離\(AH(=d)\)になっています。
(解答)
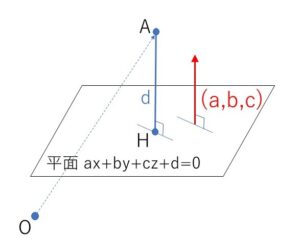
平面 \(ax+by+cz+d=0\) の法線ベクトルの1つは \((a,b,c)\) だから
\(\overrightarrow{AH}=k(a,b,c)\) と表せる。
\(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{AH}\)
\(=(x_0,y_0,z_0)+k(a,b,c)\)
\(=(x_0+ka,y_0+kb,z_0+kc)\)
\(H\)は平面 \(ax+by+cz+d=0\) 上にあるので
\(a(x_0+ka)+b(y_0+kb)+c(z_0+kc)+d=0\)
\(k(a^2+b^2+c^2)=-(ax_0+by_0+cz_0+d)\)
よって
\(k=-\displaystyle\frac{ax_0+by_0+cz_0+d}{a^2+b^2+c^2}\)
したがって
\(|\overrightarrow{AH}|=|k(a,b,c)|\)
\(=|k||(a,b,c)|\)
\(=\left|\displaystyle\frac{ax_0+by_0+cz_0+d}{a^2+b^2+c^2}\right|\sqrt{a^2+b^2+c^2}\)
\(=\displaystyle\frac{|ax_0+by_0+cz_0+d|}{a^2+b^2+c^2}\sqrt{a^2+b^2+c^2}\)
\(=\displaystyle\frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}\)
(例題2)
座標空間で、\(xy\)平面を\(α\)とし、原点\(O\)を通り \(\vec{n}=(0,2,-1)\) に垂直な平面を\(β\)、点\(A\)を (\(3,5,5)\) とすると、\(β\)は\(x\)軸と\(yz\)平面上の直線 \(z=2y\) を含む平面であり、点\(A\)は\(β\)の下側にある。
(1)平面\(β\)に関する\(A\)の対称点は \(C(3,□,□)\) である。
(2)平面\(α,β\)上にそれぞれ動点\(P,Q\)をとるとき、3線分の長さの和 \(l=AP+PQ+QA\) が最小になるのは \(Q(□,□,□)\) のときであり、\(l\)の最小値は \(\sqrt{□}\) である。
動点が平面上にあるので、平面に対称な点を考えることがポイントになります。
平面\(β\)についてはわざわざ位置関係の記述がされているので、これをもとに図を考えます。
(解答)
(1)
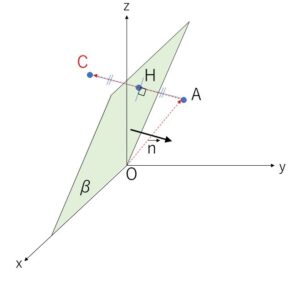
\(AC\)と平面\(β\)の交点を\(H\)とすると、
\(AH=CH\), \(平面β \perp AH\)
よって \(\overrightarrow{AH}=k(0,2,-1)\) とおけて
\(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{AH}\)
\(=(3,5,5)+k(0,2,-1)\)
\(=(3,5+2k,5-k)\)・・・①
また平面\(β\)は、原点を通り法線ベクトルが \((0,2,-1)\) なので、その方程式は
\(2y-z=0\)・・・②
\(H\)は\(β\)上にあるので①を②に代入して
\(2(5+2k)-(5-k)=0\)
\(k=-1\)
したがって
\(\overrightarrow{AH}=(0,-2,1)\) となるから
\(\overrightarrow{OC}=\overrightarrow{OA}+2\overrightarrow{AH}\)
\(=(3,5,5)+2(0,-2,1)\)
\(=(3,1,7)\)
ゆえに \(C(3,1,7)\)
(2)
(\(QA=QC\)になることについては、\(△QHA≡△QHC\) から分かります)
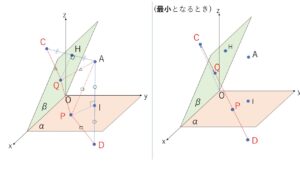
まず、平面\(α\)(\(xy\)平面)に関する\(A(3,5,5)\)の対称点\(D\)の座標は
\(D(3,5,-5)\)
すると
\(l=AP+PQ+QA\)
\(=DP+PQ+QC\)
となるから、\(l\)の最小値は\(D,P,Q,C\)が一直線上にあるときで、最小値は\(DC\)。
\(C(3,1,7)\), \(D(3,5,-5)\) より
(最小値)\(=\sqrt{0^2+4^2+(-12)^2}\)
\(=4\sqrt{10}\)
また \(\overrightarrow{CD}=(0,4,-12)\) だから
\(\overrightarrow{OQ}=\overrightarrow{OC}+m\overrightarrow{CD}\)
\(=(3,1,7)+m(0,4,-12)\)
\(=(3,1+4m,7-12m)\)・・・③
\(Q\)は 平面\(β:2y-z=0\) 上にあるので、
\(2(1+4m)-(7-12m)=0\)
\(m=\displaystyle\frac{1}{4}\)
③より
\(Q(3,2,4)\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→平面と直線・平面のなす角、平面と平面の交線 back→平面に下した垂線①