平面と直線のなす角、平面と平面のなす角、平面と平面の交線に関する例題について見ていきます。
(例題1)
直線\(l:x+1=\displaystyle\frac{y-1}{3}=\displaystyle\frac{1-z}{2}\) と、平面\(π:2x-y+3z=3\) のなす角\(θ\) (\(0°≦θ≦90°\)) を求めよ。
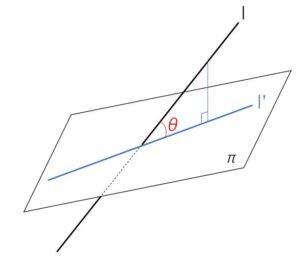
直線\(l\)から平面\(π\)へ落とした影で作られる直線を\(l’\)とします(正射影)。\(l\)と\(l’\)のなす角が、直線と平面のなす角です。(\(θ=90°\)のときは垂線として別途考える)
正射影についてもう少し詳しく説明すると、直線\(l\)の各点から平面\(π\)に下ろした垂線の足の集合が正射影です。
(解答)
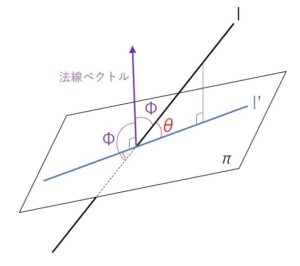
影である\(l’\)の方向ベクトルを求めるのは大変ですが、平面の法線ベクトルは簡単に分かるので、一旦法線ベクトルと\(l\)の方向ベクトルのなす角\(Φ\)を求めます。なす角\(θ\)と\(Φ\)の関係は、\(Φ≦90°\) のときは \(θ=90°-Φ\)、\(Φ>90°\) のときは \(θ=Φ-90°\) で計算します(図で判断して下さい)。
直線\(l:x+1=\displaystyle\frac{y-1}{3}=\displaystyle\frac{1-z}{2}\) と、平面\(π:2x-y+3z=3\) について
\(l:\displaystyle\frac{x+1}{1}=\displaystyle\frac{y-1}{3}=\displaystyle\frac{z-1}{-2}\) より、方向ベクトルは \(\vec{u}=(1,3,-2)\)
また平面\(π\)の法線ベクトルは \(\vec{n}=(2,-1,3)\)
\(\vec{u},\vec{n}\)のなす角を\(Φ\)とすると
\(\cosΦ=\displaystyle\frac{2-3-6}{\sqrt{14}\sqrt{14}}\)
\(=-\displaystyle\frac{1}{2}\)
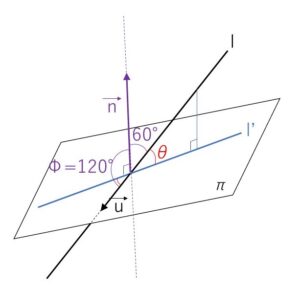
よって\(Φ=120°\)だから
\(θ=120°-90°=\)\(30°\)
(もしくは、法線と直線\(l\)(ベクトルではない)のなす角を \(180°-120°=60°\) として、\(θ=90°-60°=30°\) としてもよいです)
(例題2)
平面\(α:2x+y-z=3\), 平面\(β:x-y-2z=3\) について
(1)平面\(α,β\)のなす角\(θ\) (\(0°≦θ≦90°\)) を求めよ。
(2)平面\(α,β\)の交線の方程式を求めよ。
(3)平面\(α,β\)の交線を含み、原点\(O\)を通る平面の方程式を求めよ。
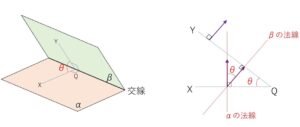
平面\(α\)と平面\(β\)のなす角\(θ\)とは、「2平面の交線と垂直になるように平面\(α,β\)それぞれに引いた2直線のなす角」です。特に、このなす角\(θ\)が直角になるとき2平面は垂直であるといいます(直交するともいう)。
今回も法線がポイントなりますが、2平面についてどちらも\(90°\)変化させたものを考えるので、法線のなす角がそのまま2平面のなす角になります。(ベクトルのなす角で考えると、\(90°\)を超える場合があるのでそのときは\(180°\)から引くことにになります)
(解答)
(1)
平面\(α:2x+y-z=3\), 平面\(β:x-y-2z=3\) について、それぞれの法線ベクトルを\(\vec{a},\vec{b}\) とおくと
\(\vec{a}=(2,1,-1)\), \(\vec{b}=(1,-1,-2)\)
\(\vec{a},\vec{b}\)のなす角を\(Φ\)とすると
\(\cosΦ=\displaystyle\frac{2-1+2}{\sqrt{6}\sqrt{6}}\)
\(=\displaystyle\frac{1}{2}\)
よって \(Φ=60°(≦90°)\) だから
\(θ=60°\)
(2)
\(α:2x+y-z=3\)・・・①
\(β:x-y-2z=3\)・・・②
①+②より
\(3x-3z=6\)
よって \(x=z+2\)・・・③
①×2-②より
\(3x+3y=3\)
よって \(x=-y+1\)・・・④
③④より交線の方程式は
\(x=-y+1=z+2\)
(3)
平面座標でやった2円の交点を通る円の方程式を求めるときと同様に、2平面の方程式を \(f(x,y,z)=0\), \(g(x,y,z)=0\) とすると、2平面の交線を通る平面の方程式は、\(kf(x,y,z)+g(x,y,z)=0\) と表すことができます。
\(α:2x+y-z-3=0\)
\(β:x-y-2z-3=0\)
平面\(α,β\)の交線を通る平面の方程式は、\(k\)を定数として
\(k(2x+y-z-3)+(x-y-2z-3)=0\)・・・⑤
と表せる。(\(α\)自身は表せないが、\(α\)は原点を通らないので求める方程式にはならない)
⑤は原点\(O(0,0,0)\)を通るので
\(-3k-3=0\)
\(k=-1\)
したがって求める平面の方程式は⑤より
\(x+2y+z=0\)
(例題3)
2つの平面 \(α:3x-z=3\), \(β:2x+y-2z=4\) に垂直で、点\((1,-2,3)\)を通る平面\(γ\)の方程式を求めよ。
(解答)
平面\(γ\)の法線ベクトルを\(\vec{n}=(a,b,c)\)とする。
\(\vec{n}\)は、平面\(α,β\)の法線ベクトル \((3,0,-1)\), \((2,1,-2)\) に垂直なので
\(3a-c=0\)・・・① \(2a+b-2c=0\)・・・②
①より \(c=3a\)
②より \(2a+b-6a=0\)
よって \(b=4a\)
ゆえに \(\vec{n}=(a,4a,3a)\)
\(a=1\) として平面\(γ\)の法線ベクトルを \((1,4,3)\) とすると、点\((1,-2,3)\)を通ることから\(γ\)の方程式は
\((x-1)+4(y+2)+3(z-3)=0\)
\(x+4y+3z-2=0\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→球面の方程式① back→平面に下ろした垂線②(点と平面の距離)