球面の方程式について見ていきます。
・球面の方程式(中心からの距離\(r\))
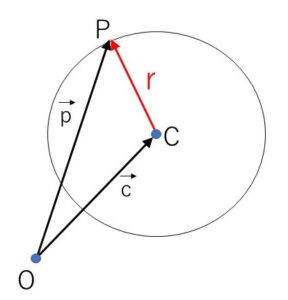
定点\(C(\vec{c})\)を中心とする半径\(r\)の球面上の点を\(P(\vec{p})\)とすると
\(|\overrightarrow{CP}|=r\)・・・①
よって
\(|\vec{p}-\vec{c}|=r\) (球面のベクトル方程式)
または、2乗すると
\((\vec{p}-\vec{c})\cdot(\vec{p}-\vec{c})=r^2\) (球面のベクトル方程式,2乗型)
ここで座標空間において球面の方程式がどうなるかを考えます。
\(C(a,b,c)\)、\(P(x,y,z)\) とおくと、\(\overrightarrow{CP}=(x-a,y-b,z-c)\) となるから①を2乗した式から
\((x-a)^2+(y-b)^2+(z-c)^2=r^2\)・・・② (球面の方程式,座標型)
(②の左辺は\(CP\)の距離の2乗になっています)
特に中心が原点\(O(0,0,0)\)であるときは
\(x^2+y^2+z^2=r^2\)
となります。
さらに②式を展開すると
\(x^2+y^2+z^2-2ax-2by-2cz+a^2+b^2+c^2-r^2=0\)
ここで\(x,y,z\)の項の係数と定数項を\(A,B,C,D\)と置き換えると
\(x^2+y^2+z^2+Ax+By+Cz+D=0\)・・・③ (球面の方程式,一般形)
(\(x^2,y^2,z^2\)の係数が等しく、他に2次の項はない形になっている)
なお、\(a^2+b^2+c^2-D=r^2>0\) より
\(\displaystyle\frac{A^2}{4}+\displaystyle\frac{B^2}{4}+\displaystyle\frac{C^2}{4}-D>0\) となるので
\(A^2+B^2+C^2-4D>0\)・・・④
が③が球面の方程式になる条件です。この条件を満たさないと③の表す図形は点になるか、存在しないことになります。
それと球面というのは、中身がスカスカな表面だけのボールがイメージです。中身が詰まったものは円の内部のように不等式で表されることになります。
・球面の方程式(直径\(AB\))
定点\(A(\vec{a})\)、\(B(\vec{b})\)について、線分\(AB\)を直径とする球面の方程式を考えます。\(A,B\)を通るような平面で球面を切断すると円になりますが、球面の中心を通るので\(A,B\)を通るどの平面で切ったときも大円になります。
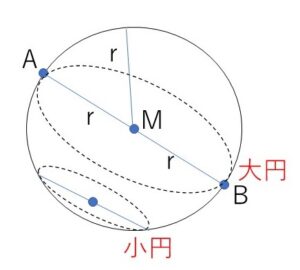
球面を平面で切断すると色々な大きさの円ができますが、大円とはこれらの円のうち最も半径が大きい円で、円の半径は球面の半径と同じになります。これより小さい半径の円は小円といいます。球面の中心を通るような平面で切断すると大円となります。
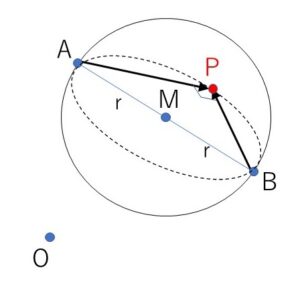
線分\(AB\)はこの大円の直径にもなるので、
\(\overrightarrow{AP}\perp\overrightarrow{BP}\) または \(A=P\) または \(B=P\)
よって、次の等式が成り立つことになります。
\(\overrightarrow{AP}\cdot\overrightarrow{BP}=0\)
したがって
\((\vec{p}-\vec{a})\cdot(\vec{p}-\vec{b})=0\)・・・④ (球面のベクトル方程式,直径型)
また④式は次のように導くこともできます。
\(A,B\)の中点は球面の中心で、その位置ベクトルは \(\displaystyle\frac{\vec{a}+\vec{b}}{2}\)
球面の半径は \(|\vec{b}-\displaystyle\frac{\vec{a}+\vec{b}}{2}|=\displaystyle\frac{|\vec{b}-\vec{a}|}{2}\)
よって、球面の方程式は
\(|\vec{p}-\displaystyle\frac{\vec{a}+\vec{b}}{2}|=\displaystyle\frac{|\vec{b}-\vec{a}|}{2}\)
となり、2乗して変形していくと
\((\vec{p}-\displaystyle\frac{\vec{a}+\vec{b}}{2})\cdot(\vec{p}-\displaystyle\frac{\vec{a}+\vec{b}}{2})=\displaystyle\frac{(\vec{b}-\vec{a})\cdot(\vec{b}-\vec{a})}{4}\)
\(|\vec{p}|^2-(\vec{a}+\vec{b})\cdot\vec{p}+\vec{a}\cdot\vec{b}=0\)
\((\vec{p}-\vec{a})\cdot(\vec{p}-\vec{b})=0\)
となり④が導かれます。
(例題)
\(x^2+y^2+z^2+6x-3y+z+11=0\) の表す図形を求めよ。
(解答)
\(x^2+6x+y^2-3y+z^2+z+11=0\)
\((x+3)^2+(y-\displaystyle\frac{3}{2})^2+(z+\displaystyle\frac{1}{2})^2-9-\displaystyle\frac{9}{4}-\displaystyle\frac{1}{4}+11=0\)
\((x+3)^2+(y-\displaystyle\frac{3}{2})^2+(z+\displaystyle\frac{1}{2})^2=(\displaystyle\frac{1}{\sqrt{2}})^2\)
よって、中心\((-3,\displaystyle\frac{3}{2},-\displaystyle\frac{1}{2})\)、半径\(\displaystyle\frac{1}{\sqrt{2}}\) の球面
本格的な演習は次回に回します。
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→球面の方程式② back→平面と直線・平面のなす角、平面と平面の交線