数列の極限の基礎

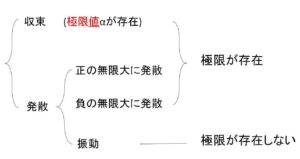
数列の極限の基礎事項について見ていきます。

・数列の極限
\(a_n=\displaystyle\frac{1}{n}\) で表される数列

\(\{a_n\}:1,\displaystyle\frac{1}{2},\displaystyle\frac{1}{3},\displaystyle\frac{1}{4},\cdots\)

は、\(n\)を限りなく大きくすると分母が限りなく大きくなり、数列\(a_n\)としては\(0\)に限りなく近づきます。
このように、数列(無限数列)\(\{a_n\}\)において、\(n\)を限りなく大きくするとき、\(a_n\)が一定の値(有限の値)\(α\)に限りなく近づくとき、数列\(\{a_n\}\)は\(α\)に収束する、または極限は\(α\)であるといいます。また収束するときの値\(α\)を極限値といいます。そしてこれらのことを式で表すと次のようになります。

「\(\displaystyle\lim_{n \to \infty}a_n=α\)」
または
「\(n \to \infty\) のとき \(a_n \to α\)」

数列\(\{a_n\}\)が\(α\)に収束する場合を数直線上で考えると、点\(a_n\)と点\(α\)の距離\(|a_n-α|\)が\(n\)を大きくすればいくらでも小さくなる(\(0\)に近づく)ということなので、\(a_n\)が\(α\)に収束することを次のように表すこともできます。

\(\displaystyle\lim_{n \to \infty}|a_n-α|=0\)

数列が収束しない場合もあります。例えば \(a_n=2n+3\) で表される数列
\(\{a_n\}:5,7,9,11,13,\cdots\)
は、\(n\)を限りなく大きくすると、限りなく大きくなります。このように\(n\)を限りなく大きくすると\(a_n\)が限りなく大きくなるとき、数列\(\{a_n\}\)は正の無限大に発散するといい次のように表します。

\(\displaystyle\lim_{n \to \infty}a_n=\infty\)
または
\(n \to \infty\) のとき \(a_n \to \infty\)

同様に \(a_n=-3n+1\) で表される数列
\(\{a_n\}:-2,-5,-8,-11,\cdots\)
は、\(n\)が大きくなると負の値であり、\(n\)が限りなく大きくなるとその絶対値\(|a_n|\)が限りなく大きくなります。この場合数列\(\{a_n\}\)は負の無限大に発散するといい次のように表します。

\(\displaystyle\lim_{n \to \infty}a_n=-\infty\)
または
\(n \to \infty\) のとき \(a_n \to -\infty\)

さらに、収束や正や負の無限大に発散しない場合もあります。

\(a_n=n\cdot(-1)^n\) で表される数列
\(\{a_n\}:-1,2,-3,4,-5,\cdots\)
は、\(n\)を限りなく大きくすると絶対値としては大きくなりますが、負の値と正の値をいったりきたりするので、収束もせず正の無限大にも負の無限大にも発散しません。このような場合、数列\(\{a_n\}\)は振動するといい、振動する数列には極限は存在しません。つまり、\(\displaystyle\lim_{n \to \infty}a_n\)は存在しないことになります。なお、振動する数列は分類としては発散に該当します。(収束しないものは発散に該当する)

以上のことをまとめると次のようになります。

・極限の性質
数列が収束する場合には、有限の値のときのように和や積などをとることができます。
つまり、数列\(\{a_n\},\{b_n\}\)が収束して
\(\displaystyle\lim_{n \to \infty}a_n=α\),  \(\displaystyle\lim_{n \to \infty}b_n=β\) のとき

①定数倍
\(\displaystyle\lim_{n \to \infty}ka_n=kα\)　(\(k\)は定数)

②和・差
\(\displaystyle\lim_{n \to \infty}(a_n±b_n)=α±β\)
①②をまとめて
\(\displaystyle\lim_{n \to \infty}(ka_n±lb_n)=kα±lβ\)　(\(k,l\)は定数)

③積
\(\displaystyle\lim_{n \to \infty}(a_nb_n)=αβ\)

④商
\(β≠0\) のとき
\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{a_n}{b_n}=\displaystyle\frac{α}{β}\)

(参考)指数の収束
\(\displaystyle\lim_{n \to \infty}a_n^{b_n}=α^β\)
(これは対数をとることで、積の形に帰着できることから分かります)

・不定形
\(\displaystyle\lim_{n \to \infty}(n^2-\displaystyle\frac{1}{n})=\infty-0\)
と形式的に書くことにすると、この例だと正の無限大に発散することは分かりますが、次のような形の極限はそのままの形では分からず、式変形が必要になってきます。

\(\infty-\infty\),　\(0×\infty\),　\(\displaystyle\frac{\infty}{\infty}\),　\(\displaystyle\frac{0}{0}\)

これらは不定形の極限といい、極限がすぐに分からないのは「極限が打ち消しあう方向に向かっていることと、発散や\(0\)に近づくスピードの違い(強さの違い)」が原因です。

例えば、\(\displaystyle\frac{0}{0}\) を例にとると
\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{\displaystyle\frac{1}{n^2}}{\displaystyle\frac{1}{n}}=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}=0\)　(分子のほうが強く\(0\)に近づく)

\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{\displaystyle\frac{1}{n}}{\displaystyle\frac{1}{n^2}}=\displaystyle\lim_{n \to \infty}n=\infty\)　(分母のほうが強く\(0\)に近づく)

であり、収束や発散のどちらの場合もあり得ます。

一方

\(\infty+\infty=\infty\),　\(\infty×\infty=\infty\),  \(-\infty×\infty=-\infty\),
\(0×0=0\),  \(\displaystyle\frac{\infty}{+0}=\infty\),  \(\displaystyle\frac{0}{\infty}=0\)

などの形の極限は不定形でなくすぐに分かる形になっています。その理由は、これらの形は不定形のときと違って和や積や商の極限が同じ方向(打ち消しあわない方向)に向かっているからです。

・極限の大小関係
数列の大小関係と極限について次のことが成り立ちます。(\(n\)は自然数)

①
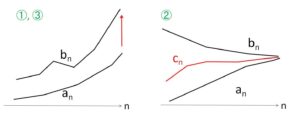
すべての\(n\)で \(a_n≦b_n\) (\(a_n<b_n\) でもよい) のとき
\(\displaystyle\lim_{n \to \infty}a_n=α\),  \(\displaystyle\lim_{n \to \infty}b_n=β\) ならば \(α≦β\)

②はさみうちの原理
すべての\(n\)で \(a_n≦c_n≦b_n\) (不等号は＝なしでもよい)のとき、
\(\displaystyle\lim_{n \to \infty}a_n=\displaystyle\lim_{n \to \infty}b_n=α\) ならば \(\displaystyle\lim_{n \to \infty}c_n=α\) (収束)

③追い出しの原理
すべての\(n\)で \(a_n≦b_n\) (\(a_n<b_n\) でもよい) のとき
\(\displaystyle\lim_{n \to \infty}a_n=\infty\) ならば \(\displaystyle\lim_{n \to \infty}b_n=\infty\) (発散)

これらのことを視覚的に表すと次のようになります。

(注)
①で\(a_n<b_n\)の場合も、極限値としては\(α≦β\)とイコールがつく。 (\(α<β\) と結論づけるは誤り) 例えば、\(a_n=\displaystyle\frac{1}{n}\),  \(b_n=\displaystyle\frac{2}{n}\) だと、\(a_n<b_n\) であるが、\(α=β=0\)。(有限な\(n\)の場合で不等号にイコールがつかなくても、極限値(近づく値)としては同じになる可能性があるので等号が必要になる)

似たような理由で②についても、\(a_n<c_n<b_n\) や \(a_n≦c_n<b_n\) という条件でもよく、このときも、\(c_n\)は両側と同じ極限値に収束する。

②は両側から、③は片側から極限がおさえつけられているイメージをもつとよい。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→数列の極限の基礎例題①(分数式など)