漸化式と極限に関する例題です。
今回は2項間、3項間の漸化式を扱います。
(例題1)
数列\(\{a_n\}\)が
\(a_1=\sqrt{2}\), \(a_{n+1}=\sqrt{a_n+2}\) (\(n=1,2,3,\cdots\))
によって定められている。
(1)\(a_n=2\sinθ_n\), \(0<θ_n<\displaystyle\frac{π}{2}\) をみたす実数\(θ_n\)を求めよ。
(2)\(\displaystyle\lim_{n \to \infty}a_n\) を求めよ。
(解答)
(1)
\(a_{n+1}=\sqrt{a_n+2}\) と \(a_n=2\sinθ_n\) より
\(2\sinθ_{n+1}=\sqrt{2\sinθ_n+2}\)
(ルートを外すために、\(\sin\)を\(\cos\)に変換して、倍角・半角の公式を使います)
\(2\sinθ_{n+1}=\sqrt{2(\sinθ_n+1)}\)
\(2\sinθ_{n+1}=\sqrt{2(\cos(\displaystyle\frac{π}{2}-θ_n)+1)}\)
\(2\sinθ_{n+1}=\sqrt{2\cdot2\cos^2\displaystyle\frac{(\displaystyle\frac{π}{2}-θ_n)}{2}}\)
\(\sinθ_{n+1}=\left|\cos(\displaystyle\frac{π}{4}-\displaystyle\frac{θ_n}{2})\right|\)
\(0<θ_n<\displaystyle\frac{π}{2}\) より
\(0<\displaystyle\frac{π}{4}-\displaystyle\frac{θ_n}{2}<\displaystyle\frac{π}{4}\) だから、絶対値がそのまま外せて
\(\sinθ_{n+1}=\cos(\displaystyle\frac{π}{4}-\displaystyle\frac{θ_n}{2})\)
(角の中身を比べるためにさらに右辺を\(\sin\)にして)
\(\sinθ_{n+1}=\sin\{\displaystyle\frac{π}{2}-(\displaystyle\frac{π}{4}-\displaystyle\frac{θ_n}{2})\}\)
\(\sinθ_{n+1}=\sin(\displaystyle\frac{θ_n}{2}+\displaystyle\frac{π}{4})\)・・・①
ここで、\(\displaystyle\frac{π}{4}<\displaystyle\frac{θ_n}{2}+\displaystyle\frac{π}{4}<\displaystyle\frac{π}{2}\) 、\(0<θ_{n+1}<\displaystyle\frac{π}{2}\) だから、①より角を比べて
\(θ_{n+1}=\displaystyle\frac{θ_n}{2}+\displaystyle\frac{π}{4}\)・・・②
(あとは漸化式②を解いて\(θ_n\)を求めるだけです)
\(a_1=\sqrt{2}\) だから
\(\sqrt{2}=2\sinθ_1\)
よって、\(θ_1=\displaystyle\frac{π}{4}\)
漸化式②の特性方程式
\(x=\displaystyle\frac{x}{2}+\displaystyle\frac{π}{4}\) を解くと
\(x=\displaystyle\frac{π}{2}\) だから②は次のように変形できる。
\(θ_{n+1}-\displaystyle\frac{π}{2}=\displaystyle\frac{1}{2}(θ_n-\displaystyle\frac{π}{2})\)
ゆえに
\(θ_{n}-\displaystyle\frac{π}{2}=\displaystyle\frac{1}{2^{n-1}}(θ_1-\displaystyle\frac{π}{2})\)
したがって
\(θ_n=-\displaystyle\frac{π}{4}\cdot\displaystyle\frac{1}{2^{n-1}}+\displaystyle\frac{π}{2}\)
(2)
\(\displaystyle\lim_{n \to \infty}a_n\)
\(=\displaystyle\lim_{n \to \infty}2\sin(-\displaystyle\frac{π}{4}\cdot\displaystyle\frac{1}{2^{n-1}}+\displaystyle\frac{π}{2})\)
\(=2\sin\displaystyle\frac{π}{2}\)
\(=2\)
(参考1)
誘導が無い場合には、まず極限を予想して証明する流れになります。
仮に数列がある値\(α\)に収束するとして、漸化式から
\(α=\sqrt{α+2}\)・・・(i)
\(α^2=α+2\)
これを解くと \(α=2,-1\) となり、(i)より\(α=2\)が極限値の予想となります。
そこで、\(\displaystyle\lim_{n \to \infty}|a_n-2|=0\) を目標として、漸化式から \(|a_{n+1}-2|\) を計算すると
\(|a_{n+1}-2|=\left|\sqrt{a_n+2}-2\right|\)
(有理化して)
\(=\left|\displaystyle\frac{a_n-2}{\sqrt{a_n+2}+2}\right|\)
\(=\left|\displaystyle\frac{1}{\sqrt{a_n+2}+2}\right||a_n-2|\)
\(\sqrt{a_n+2}≧0\) だから(条件を踏まえて、不等号なしでもよい)
\(0≦|a_{n+1}-2|≦\displaystyle\frac{1}{2}|a_n-2|\)
(1個ずれた同じ形にすることがポイント)
あとは中辺と右辺の不等式を繰り返し利用して\(n\)を下げて (普通の漸化式を解くような感覚)
\(0≦|a_{n}-2|≦\displaystyle\frac{1}{2^{n-1}}|a_1-2|\)
ゆえにはさみうちの原理から
\(\displaystyle\lim_{n \to \infty}|a_n-2|=0\)
つまり
\(\displaystyle\lim_{n \to \infty}a_n=2\)
です。
(参考2)
極限の予想はグラフを利用しても分かります。
\(a_{n+1}=\sqrt{a_n+2}\)
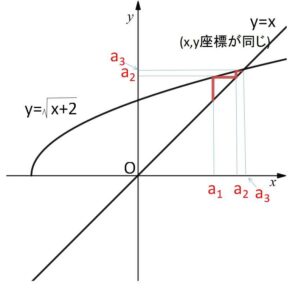
より、\(f(x)=\sqrt{x+2}\) とおくと、漸化式で\(a_2,a_3,a_4,\cdots\)と求めていく過程は
\(a_2=f(a_1)\), \(a_3=f(a_2)\), \(a_4=f(a_3)\),・・・・
となるので、関数\(y=f(x)\)の\(y\)座標が、次の項を求めるときの\(x\)座標という対応関係になっています。よって、\(y=x\) と \(y=\sqrt{x+2}\) のグラフを同時に図示すると、項を順に求める過程は図のような階段状の動きに対応します。したがって、\(a_n\)は2つのグラフの交点の\(x(y)\)座標に近づいていくことが分かります。なお交点を求めるときの方程式、\(x=\sqrt{x+2}\) は、(参考1)の\(α=\sqrt{α+2}\) と同じ形です。
(例題2)
\(a_1=r^2\), \(a_2=1\),
\(2a_{n+2}=(r+3)a_{n+1}-(r+1)a_n\) (\(n=1,2,3,\cdots\))
で定義された数列\(\{a_n\}\)が収束するような\(r\)の範囲と極限値を求めよ。
(解答)
特性方程式
\(2x^2=(r+3)x-(r+1)\) を解くと
\((x-1)\{2x-(r+1)\}=0\)
\(x=1,\displaystyle\frac{r+1}{2}\)
よって漸化式は次のように変形できる。
\(a_{n+2}-a_{n+1}=\displaystyle\frac{r+1}{2}(a_{n+1}-a_n)\)・・・①
\(a_{n+2}-\displaystyle\frac{r+1}{2}a_{n+1}=a_{n+1}-\displaystyle\frac{r+1}{2}a_n\)・・・②
(初期条件は \(a_1=r^2\), \(a_2=1\))
①より
\(\color{blue}{a_{n+1}-a_n}=\left(\displaystyle\frac{r+1}{2}\right)^{n-1}(a_2-a_1)=\color{blue}{(1-r^2)\left(\displaystyle\frac{r+1}{2}\right)^{n-1}}\)・・・③
②より
\(\color{blue}{a_{n+1}-\displaystyle\frac{r+1}{2}a_n}=a_2-\displaystyle\frac{r+1}{2}a_1=\color{blue}{\displaystyle\frac{-r^3-r^2+2}{2}}\)・・・④
③-④より
\(\displaystyle\frac{r-1}{2}a_n=(1-r^2)\left(\displaystyle\frac{r+1}{2}\right)^{n-1}+\displaystyle\frac{(r-1)(r^2+2r+2)}{2}\)
(ア)\(r≠1\) のとき、\(\displaystyle\frac{2}{r-1}\)倍して整理すると
\(a_n=-4\left(\displaystyle\frac{r+1}{2}\right)^{n}+(r^2+2r+2)\)
ゆえに\(\{a_n\}\)が収束するためには
\(-1<\displaystyle\frac{r+1}{2}≦1\)
\(r≠1\)とあわせて
\(-3<r<1\)
このとき極限値は、公比の絶対値は\(1\)未満だから
\(\displaystyle\lim_{n \to \infty}a_n=r^2+2r+2\)
(イ)\(r=1\) のとき③より(④でもよい)
\(a_{n+1}-a_n=0\) (すべての項は同じ)
つまり
\(a_n=a_1=1\)
このとき
\(\displaystyle\lim_{n \to \infty}a_n=1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→漸化式と極限②(分数型・連立型) back→極限と正誤判定