不等式を利用する無限級数の例題です。特に部分和が計算できない分数の和を扱っていきます。
(例題1)
次の極限を求めよ。
(1)\(\displaystyle\lim_{n \to \infty}\left(\displaystyle\frac{1}{n^2+1}+\displaystyle\frac{1}{n^2+2}+\cdots+\displaystyle\frac{1}{n^2+n}\right)\)
(2)\(\displaystyle\lim_{n \to \infty}\left(\displaystyle\frac{1}{\sqrt{n^2+1}}+\displaystyle\frac{1}{\sqrt{n^2+2}}+\cdots+\displaystyle\frac{1}{\sqrt{n^2+n}}\right)\)
(解答)
(1)
ここで、まず極限の予想ができるならするべきですが、項数は\(n\)で、\(n \to \infty\) のとき分母はほとんど\(n^2\)であることに着目すると、\(\displaystyle\frac{1}{n^2}\cdot n=\displaystyle\frac{1}{n}\) となるから、\(0\)に収束することが予想されます。
\(0<\displaystyle\frac{1}{n^2+1}+\displaystyle\frac{1}{n^2+2}+\cdots+\displaystyle\frac{1}{n^2+n}<\displaystyle\frac{1}{n^2}+\displaystyle\frac{1}{n^2}+\cdots+\displaystyle\frac{1}{n^2}\) より
\(0<\displaystyle\frac{1}{n^2+1}+\displaystyle\frac{1}{n^2+2}+\cdots+\displaystyle\frac{1}{n^2+n}<\displaystyle\frac{1}{n^2}\cdot n\)
よって
\(0<\displaystyle\frac{1}{n^2+1}+\displaystyle\frac{1}{n^2+2}+\cdots+\displaystyle\frac{1}{n^2+n}<\displaystyle\frac{1}{n}\)
はさみうちの原理から
\(\displaystyle\lim_{n \to \infty}\left(\displaystyle\frac{1}{n^2+1}+\displaystyle\frac{1}{n^2+2}+\cdots+\displaystyle\frac{1}{n^2+n}\right)=0\)
(2)
\(\displaystyle\frac{1}{\sqrt{n^2}}\cdot n=1\) なので、\(1\)に収束することが予想できます。\(1\)に収束するような式ではさみたいので、一番大きい項と小さい項に着目します。(右辺を \(\displaystyle\frac{1}{\sqrt{n^2}}\cdot n\) としてもよいです)
\(\displaystyle\frac{1}{\sqrt{n^2+n}}\cdot n<\displaystyle\frac{1}{\sqrt{n^2+1}}+\displaystyle\frac{1}{\sqrt{n^2+2}}+\cdots+\displaystyle\frac{1}{\sqrt{n^2+n}}<\displaystyle\frac{1}{\sqrt{n^2+1}}\cdot n\)
よって
\(\displaystyle\frac{n}{\sqrt{n^2+n}}<\displaystyle\frac{1}{\sqrt{n^2+1}}+\displaystyle\frac{1}{\sqrt{n^2+2}}+\cdots+\displaystyle\frac{1}{\sqrt{n^2+n}}<\displaystyle\frac{n}{\sqrt{n^2+1}}\)
\(\displaystyle\frac{1}{\sqrt{1+\displaystyle\frac{1}{n}}}<\displaystyle\frac{1}{\sqrt{n^2+1}}+\displaystyle\frac{1}{\sqrt{n^2+2}}+\cdots+\displaystyle\frac{1}{\sqrt{n^2+n}}<\displaystyle\frac{1}{\sqrt{1+\displaystyle\frac{1}{n^2}}}\)
はさみうちの原理から
\(\displaystyle\lim_{n \to \infty}\left(\displaystyle\frac{1}{\sqrt{n^2+1}}+\displaystyle\frac{1}{\sqrt{n^2+2}}+\cdots+\displaystyle\frac{1}{\sqrt{n^2+n}}\right)=1\)
(例題2)
(1)\(n\)桁の自然数のうち、各位の数字がすべて\(1\)と異なるものの個数を求めよ。
(2)自然数の逆数からなる級数
\(1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\cdots+\displaystyle\frac{1}{m}+\cdots\)
から、分母に数字\(1\)が現れる項をすべて除いて得られる級数
\(\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\displaystyle\frac{1}{4}+\displaystyle\frac{1}{5}+\displaystyle\frac{1}{6}+\displaystyle\frac{1}{7}+\displaystyle\frac{1}{8}+\displaystyle\frac{1}{9}+\displaystyle\frac{1}{20}+\displaystyle\frac{1}{22}+\cdots\)
の和は\(40\)を超えないことを示せ。
(解答)
(1)
\(n\)桁目の選び方は、\(2~9\)の\(8\)通り。
それ以外は\(0,2~9\)の\(9\)通りだから
\(8\cdot9^{n-1}\) 個。
(2)
(本来は部分和を考えたほうがよいですが、逆にややこしくなりそうなので簡略化した解答にします)
\(\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\displaystyle\frac{1}{4}+\displaystyle\frac{1}{5}+\displaystyle\frac{1}{6}+\displaystyle\frac{1}{7}+\displaystyle\frac{1}{8}+\displaystyle\frac{1}{9}+\displaystyle\frac{1}{20}+\displaystyle\frac{1}{22}+\cdots\)
\(<(\displaystyle\frac{1}{2}+\displaystyle\frac{1}{2}+\cdots+\displaystyle\frac{1}{2})+(\displaystyle\frac{1}{20}+\displaystyle\frac{1}{20}+\cdots+\displaystyle\frac{1}{20})+(\displaystyle\frac{1}{200}+\cdots\)
\(=\displaystyle\frac{1}{2}\cdot8\cdot9^0+\displaystyle\frac{1}{20}\cdot8\cdot9+\displaystyle\frac{1}{200}\cdot8\cdot9^2+\cdots\)
\(=4\left\{1+\displaystyle\frac{9}{10}+(\displaystyle\frac{9}{10})^2+\cdots\right\}\)
\(=4\cdot\displaystyle\frac{1}{1-\displaystyle\frac{9}{10}}\)
\(=40\)
よって無限級数は収束して、その和は\(40\)を超えない。
(参考)
似たような考え方で、自然数の逆数の級数
\(1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\displaystyle\frac{1}{4}+\cdots\)
の発散を示すことができます。(数列\(\{\displaystyle\frac{1}{n}\}\)は\(0\)に収束するが、級数は発散する例)
\(S_n=1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\cdots+\displaystyle\frac{1}{n}\)
とすると、\(\displaystyle\frac{1}{2^m}\)までの部分和について、\(m\)が十分大きいとき
\(S_{2^m}=1+\displaystyle\frac{1}{2}+(\displaystyle\frac{1}{3}+\displaystyle\frac{1}{4})+(\displaystyle\frac{1}{5}+\displaystyle\frac{1}{6}+\displaystyle\frac{1}{7}+\displaystyle\frac{1}{8})+\cdots+\displaystyle\frac{1}{2^m-1}+\displaystyle\frac{1}{2^m})\)
\(>1+\displaystyle\frac{1}{2}+(\displaystyle\frac{1}{4}+\displaystyle\frac{1}{4})+(\displaystyle\frac{1}{8}+\displaystyle\frac{1}{8}+\displaystyle\frac{1}{8}+\displaystyle\frac{1}{8})+\cdots+(\displaystyle\frac{1}{2^m}+\cdots+\displaystyle\frac{1}{2^m})\)
\(=1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{2}+\cdots+\displaystyle\frac{1}{2}\)
\(=1+\displaystyle\frac{1}{2}m\)
ここで、\(n≧2^{m}\) とすれば
\(S_n≧S_{2^{m}}>1+\displaystyle\frac{1}{2}m\)
\(m \to \infty\) のとき \(n \to \infty\) だから、\(\displaystyle\lim
_{m \to \infty}(1+\displaystyle\frac{1}{2}m)=\infty\) より
\(\displaystyle\lim_{n \to \infty}S_n=\infty\)
ただし、\(\displaystyle\sum_{n=1}^{\infty}\displaystyle\frac{1}{n^p}\) 型の無限級数の収束・発散については、積分による評価をするのが分かりやすいと思います。この例 \(\displaystyle\sum_{n=1}^{\infty}\displaystyle\frac{1}{n}\) については、部分和を考えると図より
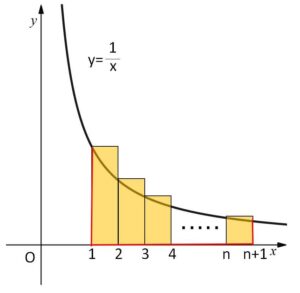
(曲線がつくる面積)<(長方形の面積の合計) だから
\(\displaystyle\int_1^{n+1}\displaystyle\frac{1}{x}dx<1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\cdots+\displaystyle\frac{1}{n}\)
よって
\(\log(n+1)<\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{k}\)
\(n \to \infty\) のとき、\(\log(n+1) \to \infty\) となるので
\(\displaystyle\sum_{n=1}^{\infty}\displaystyle\frac{1}{n}\) は発散します。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→無限級数と順序交換 back→(等差)×(等比)型の無限級数