関数の極限の基礎

関数の極限の基礎知識について整理します。

・関数の極限(\(x \to \infty\), \(x \to -\infty\))
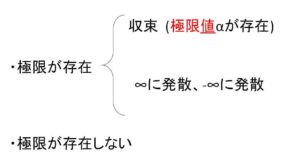
数列の極限と同様に、\(x\)を限りなく大きくするとき(\(x \to \infty\)のとき)、関数\(f(x)\)の値が一定値\(α\)に近づく場合、「\(x \to \infty\)のとき \(f(x)\) は \(α\) に収束する」といい、この\(α\)を「\(x \to \infty\) のときの \(f(x)\) の極限」といい、\(\displaystyle\lim_{x \to \infty}f(x)=α\) と表します。収束する場合の一定値\(α\)は特に極限値とよばれます。例えば \(\displaystyle\lim_{x \to \infty}\displaystyle\frac{1}{x}=0\) です。

収束しない場合ももちろんあり、\(x \to \infty\) のとき\(f(x)\)の値が限りなく大きくなるときは、「\(x \to \infty\) のとき \(f(x)\) は 正の無限大に発散する」といい、\(\displaystyle\lim_{x \to \infty}f(x)=\infty\) と表します。この場合の極限は\(\infty\)(正の無限大)になります。同様に\(x \to \infty\) のとき\(f(x)\)が負の値でその絶対値が大きくなるときは、「\(x \to \infty\) のとき \(f(x)\) は 負の無限大に発散する」といい、\(\displaystyle\lim_{x \to \infty}f(x)=-\infty\) と表します。この場合の極限は\(-\infty\)(負の無限大)になります。例を挙げると、\(\displaystyle\lim_{x \to \infty}2x=\infty\)、\(\displaystyle\lim_{x \to \infty}(-x)=-\infty\) です。なお、極限\(±\infty\)を極限値とよばないこと、\(\infty\)を正であることを強調して\(+\infty\)と書く場合もあるのは数列の極限と同様です。

また \(\displaystyle\lim_{x \to \infty}\cos x\) のように、収束もせず、正の無限大にも負の無限大にも発散しない場合、極限は存在しないといいます。

以上のことは、\(x \to -\infty\) (\(x\)が負の値でその絶対値が限りなく大きくなる) のときも同じことが言えます。

・関数の極限(\(x \to a\))
関数\(f(x)\)において、\(x\)が\(a\)と異なる値をとりながら限りなく\(a\)に近づくとき、\(f(x)\)が一定の値\(α\)に限りなく近づくとき、「\(x \to a\)のとき \(f(x)\) は \(α\) に収束する」といい、この\(α\)を「\(x \to a\) のときの \(f(x)\) の極限」といい、\(\displaystyle\lim_{x \to a}f(x)=α\) と表します。収束する場合の一定値\(α\)は特に極限値とよばれます。

ただし \(x \to a\) の極限は、\(x \to ±\infty\) のときと違って近づき方が、右方向から近づける場合と左方向から近づける場合の2パターン存在します。

\(f(x)\)において、\(x\)が\(a\)より大きい値をとりながら限りなく\(a\)に近づくとき、この場合の\(f(x)\)の極限を「\(x\)が\(a\)に近づくときの\(f(x)\)の右側極限」といい、右方向からの極限であることを強調するために近づけ方を、\(x \to a\color{red}{+0}\) と表し、極限が存在するならば、\(\displaystyle\lim_{x \to a\color{red}{+0}}=α\) や \(\displaystyle\lim_{x \to a\color{red}{+0}}=\infty\) などと表します。
左側極限も同様に定義され、\(x \to a\color{red}{-0}\) を用います。

なお、\(a=0\) の場合は \(x \to +0\)、\(x \to -0\) とします。

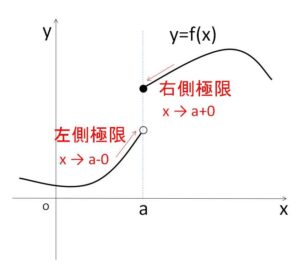
ここで、\(\displaystyle\lim_{x \to a}f(x)=α\) (一定値\(α\)に収束) の表す意味は、右側極限と左側極限がどちらも存在し、かつその極限値が\(α\)で一致するということです。よって上図のようなグラフの関数では、極限値が一致してないので \(\displaystyle\lim_{x \to a}f(x)\) は存在しないことになります(極限が存在しない)。ただし、その他の無数の点においては極限値は存在しています。

それと、\(f(a)\) と \(\displaystyle\lim_{x \to a}f(x)\) は異なるものです。上図では、右側極限 \(\displaystyle\lim_{x \to a+0}f(x)\) と \(f(a)\) は一致していますが、左側極限と \(f(a)\) は一致していません。(それにそもそも\(\displaystyle\lim_{x \to a}f(x)\) は存在していない)

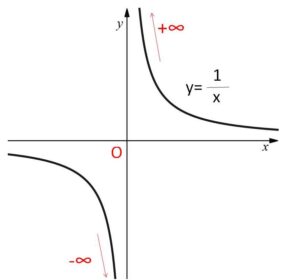
また、\(x \to a\)のときの発散についても同様に両側で極限を考えます。例えば \(f(x)=\displaystyle\frac{1}{x}\) について
\(\displaystyle\lim_{x \to +0}\displaystyle\frac{1}{x}=+\infty\)、\(\displaystyle\lim_{x \to -0}\displaystyle\frac{1}{x}=-\infty\) となるので、極限 \(\displaystyle\lim_{x \to 0}\displaystyle\frac{1}{x}\) は存在しません。

・関数の極限の性質
数列の極限と同じ性質をもちます。
\(\displaystyle\lim_{x \to a}f(x)=α\)、\(\displaystyle\lim_{x \to a}g(x)=β\)　(それぞれ収束) のとき

①定数倍・和・差
\(\displaystyle\lim_{x \to a}\{kf(x)+lg(x)\}=kα+lβ\)　(\(k,l\)は定数)

②積
\(\displaystyle\lim_{x \to a}f(x)g(x)=αβ\)

③商
\(β≠0\) のとき \(\displaystyle\lim_{x \to a}\displaystyle\frac{f(x)}{g(x)}=\displaystyle\frac{α}{β}\)

以上のことは、\(x \to \infty\)、\(x \to -\infty\) とおきかえた場合も成り立つ。

・関数の極限と大小関係
数列の場合と同様に、極限の大小関係について次のことが成り立ちます。

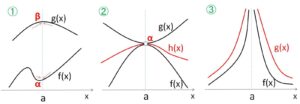
①
\(x\)が\(a\)に近いとき、常に \(f(x)≦g(x)\) が成り立つとき
\(\displaystyle\lim_{x \to a}f(x)=α\)、\(\displaystyle\lim_{x \to a}g(x)=β\) ならば
\(α≦β\)

②はさみうちの原理
\(x\)が\(a\)に近いとき、常に \(f(x)≦h(x)≦g(x)\) が成り立つとき
\(\displaystyle\lim_{x \to a}f(x)=α\)、\(\displaystyle\lim_{x \to a}g(x)=α\) ならば
\(\displaystyle\lim_{x \to a}h(x)=α\) (両側の極限値に収束する)

③追い出しの原理
\(x\)が\(a\)に近いとき、常に \(f(x)≦g(x)\) が成り立つとき
\(\displaystyle\lim_{x \to a}f(x)=\infty\) ならば
\(\displaystyle\lim_{x \to a}g(x)=\infty\)　(発散する)

なお、\(f(x),g(x),h(x)\)に関する不等式における不等号の＝は、あっても無くても結論は変わらない。例えば、①だと \(f(x)<g(x)\) の場合でも \(α≦β\) となる。(極限の不等号については＝はつく)

また以上のことは、「\(x\)の絶対値が十分大きいとき」とおきかえると、\(x \to \infty\)、\(x \to -\infty\) の場合も成り立つ。

演習は次回にします。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→関数の極限の基礎例題　back→十分大きいnと数列の収束