関数の連続・不連続

関数の連続について見ていきます。

・関数の連続・不連続

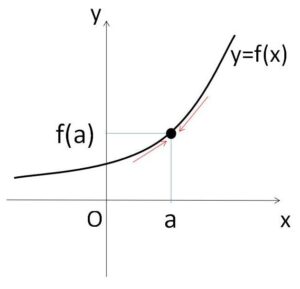
今までよく扱った2次関数や指数関数などは、上図のように定義域内の1つの値 \(x=a\) に対して
\(\displaystyle\lim_{x \to a}f(x)=f(a)\)・・・①  (極限値が存在して、さらに\(f(a)\)に一致)
が成り立ちます。

しかし次の図のように \(x=a\) において、極限値が存在しなかったり(図1)、極限値が存在しても\(f(a)\)と一致しない(図2)場合があります。

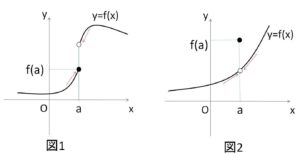
一般に、関数\(f(x)\)の定義域に属する\(x\)の値\(a\)に対して、\(x=a\)における関数の連続を次のように定義します。

そして、図1,2のように①②のいずれかが成り立たたないとき、関数\(f(x)\)は \(x=a\) において不連続であるといいます(簡単にいうとつながっていないということ)。なお、\(x=a\) が定義域に属さない場合には関数の連続性については考えないこととします。

・関数の連続に関する性質
関数の極限の性質を利用すると、同様のことが成り立つことが分かります。

関数\(f(x),g(x)\)が定義域の点 \(x=a\) で連続ならば、次のように\(f(x),g(x)\)を組み合わせて作った関数も、\(x=a\) で連続である。

①\(kf(x)+lg(x)\)　(\(k,l\)は定数)
②\(f(x)g(x)\)
③\(\displaystyle\frac{f(x)}{g(x)}\)　(ただし \(g(a)≠0\))

例えば①については、\(\displaystyle\lim_{x \to a}f(x)=f(a)\)、\(\displaystyle\lim_{x \to a}g(x)=g(a)\) だから
\(\displaystyle\lim_{x \to a}\{kf(x)+lg(x)\}=k\displaystyle\lim_{x \to a}f(x)+l\displaystyle\lim_{x \to a}g(x)=kf(a)+lg(a)\)
となり、関数 \(kf(x)+lg(x)\) も \(x=a\) で連続であることが分かる。

・区間と連続
一般に関数\(f(x)\)が定義域のすべての\(x\)について連続であるとき、\(f(x)\)は連続関数であるといいます。例えば2次関数や三角関数、指数関数、対数関数(定義域は \(x>0\) )、無理関数などは連続関数です。

次に区間における連続について考えます。

まず区間についておさらいしておくと
つぎのような不等式
\(a<x<b\)、\(a≦x<b\)、\(a<x≦b\)、\(a≦x≦b\)
を満たす実数\(x\)全体の集合をいずれも区間といい、それぞれ記号 \((\ ]\) を用いて
\((a,b)\)、\([a,b)\)、\((a,b]\)、\([a,b]\)　(\(=\)がつくとき \([\) を用いる)
で表します。とくに、\((a,b)\)を開区間、\([a,b]\)を閉区間といいます。

またつぎのような不等式
\(a<x\)、\(a≦x\)、\(x<b\)、\(x≦b\)
(\(a<x<\infty\)、\(a≦x<\infty\)、\(-\infty<x<b\)、\(\infty<x≦b\) と書く場合もある)
を満たす実数\(x\)全体の集合も区間であり、\(±\infty\) を用いることで同様に
\((a,\infty)\)、\([a,\infty)\)、\((-\infty,b)\)、\((-\infty,b]\)　(\(±\infty\)のほうは\(＝\)はつかない)
で表します。

ここで、関数\(f(x)\)がある区間\(I\)に属するすべての\(x\)において連続であるとき、\(f(x)\)は区間\(I\)において連続であるといいます。
なお端点における連続については、片側極限を考えます。\(a≦x\) (左端が含まれる)、\(a<x≦b\) (右端が含まれる)、\(a≦x≦b\) (両端が含まれる) などのように

区間が左端の点\(x=a\)を含むとき、\(\displaystyle\lim_{x \to a+0}f(x)=f(a)\) が成り立てば、\(x=a\) で連続です。(左側は区間外なので、右側極限のみを考える)

同様に、右端の点\(x=b\)を含むとき、\(\displaystyle\lim_{x \to b-0}f(x)=f(b)\) が成り立てば、\(x=b\) で連続です。(右側は区間外なので、左側極限のみを考える)

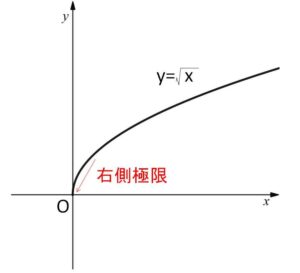
具体例を挙げると、\(f(x)=\sqrt{x}\) \((x≧0)\) の \(x=0\) における連続性については、
\(\displaystyle\lim_{x \to +0}f(x)=f(0)\ (=0)\)
より、\(x=0\) で連続となります。

(参考)
関数の極限を考える際に、\(\displaystyle\lim_{x \to 1}(x^2+x+1)=1^2+1+1=3\)
のようにあたかも代入するように扱いますが、これは \(f(x)=x^2+x+1\) の連続性によるものです。しかし、連続の判断には極限の条件  \(\displaystyle\lim_{x \to a}f(x)=f(a)\) を使うので、結局どこかで関数の極限の厳密な求める方法の検討が必要になります。ただし、高校数学の範囲ではやや感覚的なところがありますが、グラフの形状から連続性や極限の判断をしてよく、とくに\(n\)次関数、三角関数、指数関数、対数関数、無理関数などの主要な関数は特別な設定がしていない限り、連続関数として扱ってよいです。
少しだけ理屈で考えるなら、\(x=a\)からほんの少しだけ増やした(減らした)場合の、\(f(x)\)の値の変化を考えるとよいです。

(例題)
(1)
\(\begin{eqnarray} f(x) = \begin{cases} \displaystyle\frac{1-\cos x}{x} & ( x≠0 ) \\ \hspace{16pt} a & (x = 0 ) \end{cases} \end{eqnarray}\)
で定義される関数\(f(x)\)が、\(-\infty<x<\infty\) で連続となるように定数\(a\)の値を定めよ。

(2)
\(g(x)=\displaystyle\frac{[x]}{x}\)　(\(-1≦x≦2\)、\(x≠0\))
の連続性について調べよ。ただし\([x]\)は\(x\)を超えない最大の整数とする。

(解答)
(1)

\(y=x\)、\(y=1-\cos x\) は実数全体で連続なので
\(f(x)=\displaystyle\frac{1-\cos x}{x}\) (\(x≠0\)) は連続。

よって、\(x=0\) について
\(\displaystyle\lim_{x \to 0}\displaystyle\frac{1-\cos x}{x}=f(0)\ (=a)\)
であればよい。

\(\displaystyle\lim_{x \to 0}\displaystyle\frac{1-\cos x}{x}\)

\(=\displaystyle\lim_{x \to 0}\displaystyle\frac{1-\cos^2 x}{x(1+\cos x)}\)

\(=\displaystyle\lim_{x \to 0}\displaystyle\frac{\sin x}{x}\cdot\displaystyle\frac{\sin x}{1+\cos x}\)

\(=1\cdot\displaystyle\frac{0}{2}=0\)

よって
\(a=0\)

(2)

\(g(x)=\displaystyle\frac{[x]}{x}\)　(\(-1≦x≦2\)、\(x≠0\))

①\(-1≦x<0\) のとき
\([x]=-1\) だから
\(g(x)=-\displaystyle\frac{1}{x}\)

②\(0<x<1\) のとき
\([x]=0\) だから
\(g(x)=0\)

③\(1≦x<2\) のとき
\([x]=1\) だから
\(g(x)=\displaystyle\frac{1}{x}\)

④\(x=2\) のとき
\([x]=2\) だから
\(g(x)=\displaystyle\frac{2}{2}=1\)

グラフをかくと次の通り。

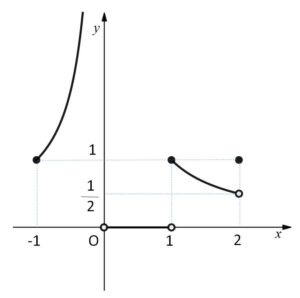
よって
\(-1≦x<0\)、\(0<x<1\)、\(1<x<2\) で連続。
\(x=1,2\) で不連続。

(\(x=0\)は定義域にないので考えない)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→極限で表された関数　back→はさみうちと関数の極限