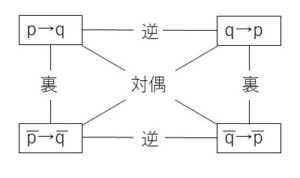
・逆・裏・対偶
命題「\(p→q\)」に対して
「\(q→p\)」を逆
「\(\overline{p}→\overline{q}\)」を裏
「\(\overline{q}→\overline{p}\)」を対偶
といいます。
逆は\(p,q\)を入れ替えたもの、裏はバーをつけたもの、対偶はバーをつけてさらに入れ替えたものになります。
(例)命題「\(x=2→x^2=4\)」(真)については
逆 「\(x^2=4→x=2\)」 (偽) (反例:\(x=-2\))
裏 「\(x≠2→x^2≠4\)」 (偽) (反例:\(x=-2\))
対偶 「\(x^2≠4→x≠2\)」 (真)
裏 「\(x≠2→x^2≠4\)」 (偽) (反例:\(x=-2\))
対偶 「\(x^2≠4→x≠2\)」 (真)
となります。
・命題とその逆(と裏)の真偽
例からもわかるように、ある命題とその逆の真偽は一致するとは限りません。
また、ある命題とその裏の真偽も一致するとは限りません。
(一致する場合もあります)
また、ある命題とその裏の真偽も一致するとは限りません。
(一致する場合もあります)
・命題とその対偶の真偽
ある命題とその対偶の真偽は必ず一致します。
ある命題とその対偶の真偽は必ず一致します。
(考え方)
集合を考えると分かります。
\(p,q\)を満たす全体の集合をそれぞれ\(P,Q\)とすると、
\(p→q\)が真
\(\leftrightarrow\) \(P\subset Q\)
\(\leftrightarrow\) \(\overline{Q}\subset \overline{P}\)
\(\leftrightarrow\) \(\overline{q}→\overline{p}\)が真
集合を考えると分かります。
\(p,q\)を満たす全体の集合をそれぞれ\(P,Q\)とすると、
\(p→q\)が真
\(\leftrightarrow\) \(P\subset Q\)
\(\leftrightarrow\) \(\overline{Q}\subset \overline{P}\)
\(\leftrightarrow\) \(\overline{q}→\overline{p}\)が真
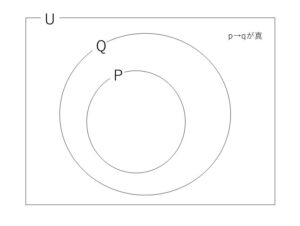
(図を変えれば\(p→q\)が偽であるときも同様に示されます)
ちなみに逆の対偶は裏なので、逆と裏の真偽も一致します。
・命題の証明と対偶
ある命題を直接証明するのが難しい場合、対偶と真偽が一致することを利用して対偶を証明することで間接的にある命題を証明する方法が有効なことがあります。
ある命題を直接証明するのが難しい場合、対偶と真偽が一致することを利用して対偶を証明することで間接的にある命題を証明する方法が有効なことがあります。
(例)
\(n\)を整数とするとき
「\(n^2\)が偶数ならば、\(n\)は偶数である」
を証明せよ。
\(n\)を整数とするとき
「\(n^2\)が偶数ならば、\(n\)は偶数である」
を証明せよ。
(解答)
証明すべき命題の対偶は、
「\(n\)が奇数ならば、\(n^2\)は奇数である」・・・①
となる。
奇数\(n\)を、ある整数\(k\)を用いて\(n=2k+1\)と表すと
\(n^2=(2k+1)^2=4(k^2+k)+1\)
\(4(k^2+k)\)は偶数であるから、\(n^2\)は奇数となる。
よって命題①は真であるので、もとの証明すべき命題も真となる。
証明すべき命題の対偶は、
「\(n\)が奇数ならば、\(n^2\)は奇数である」・・・①
となる。
奇数\(n\)を、ある整数\(k\)を用いて\(n=2k+1\)と表すと
\(n^2=(2k+1)^2=4(k^2+k)+1\)
\(4(k^2+k)\)は偶数であるから、\(n^2\)は奇数となる。
よって命題①は真であるので、もとの証明すべき命題も真となる。
「\(n^2\)が偶数」という条件が扱いにくいので、扱いやすい「\(n\)が奇数」という条件が出てくる対偶をとりました。
以上になります。お疲れさまでした。
ここまで読んで頂きありがとうございました。
ここまで読んで頂きありがとうございました。