2次方程式が2つの実数解をもち、その2解がある数より大きい(または小さい)場合の条件を考えます。正の解、負の解は\(0\)より大きいまたは小さい解なので、前回(→正の解・負の解)学習した、正の解・負の解をもつ条件とほぼ同じように求めることができます。
・2解がある数\(k\)よりともに大きい条件
正の解を2つもつ条件では、①判別式の符号、②\(y\)軸 (つまり \(x=0\))と軸の関係、③\(f(0)\)の符号 について考えましたが、正の解は言い換えれば\(0\)より大きい解なので、\(y\)軸をそのまま\(x=k\)にすりかえることで2解がともに\(k\)より大きい条件を考えることができます。
2次方程式 \(ax^2+bx+c=0\) (ただし\(a>0\))が2つの異なる実数解(重解を含む)をもち、その2解がともに\(k\)より大きい値をとる条件について考えていきます。2解を2次関数のグラフと\(x\)軸の交点の\(x\)座標として考えるために、\(y=f(x)=ax^2+bx+c\) とおくと、条件を満たすグラフは次の通りです。
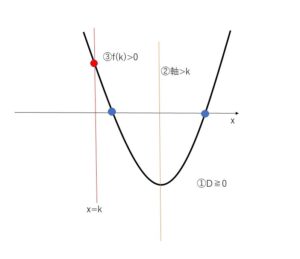
よって2解が\(k\)よりも大きくなる条件は
①判別式 \(D≧0\)
②軸\(>k\)
③\(f(k)>0\)
・2解がある数\(k\)よりともに小さい条件
2次方程式 \(ax^2+bx+c=0\) (ただし\(a>0\))が2つの異なる実数解(重解を含む)をもち、その2解がともに\(k\)より小さい値をとる条件について考えていきます。2解を2次関数のグラフと\(x\)軸の交点の\(x\)座標として考えるために、\(y=f(x)=ax^2+bx+c\) とおくと、条件を満たすグラフは次の通りです。
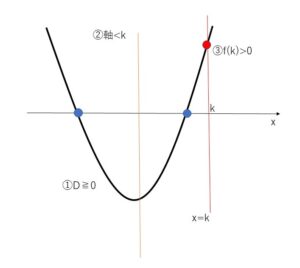
よって2解が\(k\)よりも小さくなる条件は
①判別式 \(D≧0\)
②軸\(<k\)
③\(f(k)>0\)
・2解のうち1つが\(k\)より小さく、もう1つは\(k\)より大きい条件
2次方程式 \(ax^2+bx+c=0\) (ただし\(a>0\))が2つの異なる実数解をもち、その2解のうち1つが\(k\)より小さく、もう1つが\(k\)より大きい値をとる条件について考えていきます。
\(y=f(x)=ax^2+bx+c\) とおくと、条件を満たすグラフは次の通りです。
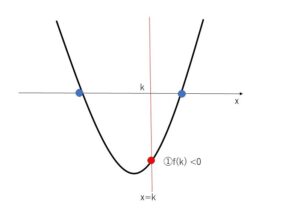
条件は
①\(f(k)<0\)
です。
(例題)
\(x\)の2次方程式 \(x^2-(a+7)x+a^2=0\) が\(1\)より大きな解と\(1\)より小さな解を1つずつもつための定数\(a\)の値の範囲を求めよ。
(解答)
\(f(x)=x^2-(a+7)x+a^2\) とおくと、グラフは下に凸の放物線であり、求める条件は
\(f(1)=1-(a+7)+a^2<0\) より
\(a^2-a-6<0\) \((a+2)(a-3)<0\) より
\(-2<a<3\)
以上なります。 お疲れさまでした。
ここまで見て頂きありがとうございました。