与えられた条件から、2次関数の方程式を求める方法について考えていきます。ここでは、2次関数の方程式を最初にどう設定するかが大事になってきます。
・頂点・軸が与えられた場合
頂点・軸が与えられた場合は、標準形 \(y=a(x-p)^2+q\) を用います。条件を\(p,q\)にダイレクトに代入できるからです。
(例題1)
軸の方程式が \(x=-1\)で、2点\((-2,9)\), \((1,3)\) を通る2次関数を求めよ。
(解答)
求める2次関数は
\(y=a(x+1)^2+q\)
2点をそれぞれ代入して
\(9=a+q\) \(3=4a+q\)
よって \(a=-2,q=11\)
したがって、2次関数は \(y=-2(x+1)^2+11\)
・3点が与えられた場合
3点が与えられた場合、一般形 \(y=ax^2+bx+c\) を使います。それぞれの座標を代入すると、文字3つの式が3つできて連立すると具体的に\(a,b,c\)の値が求まります。
(例題2)
3点 \((-1,6),(1,4),(2,9)\) を通る2次関数を求めよ。
(解答)
求める2次関数を \(y=ax^2+bx+c\) とおく。
3点の座標を代入して
\(6=a-b+c\)・・・①
\(4=a+b+c\)・・・②
\(9=4a+2b+c\)・・・③
②-①から
\(-2=2b\) よって \(b=-1\)
③-②から
\(5=3a+b\) \(b=-1\)から \(a=2\)
①に\(a=2,b=-1\)を代入して \(c=3\)
以上から、2次関数は \(y=2x^2-x+3\)
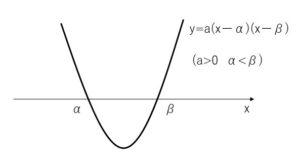
・2点 \((α,0),(β,0)\) (\(x\)軸との共有点) が与えられた場合
求める関数を \(y=ax^2+bx+c\) とすると、\(α,β\)は2次方程式 \(0=ax^2+bx+c\)
の2解となります。よって \(y=ax^2+bx+c\) は \(y=a(x-α)(x-β)\) と変形することができます。(→2次方程式の解の利用 を参照) ちなみに2点 \((α,0),(β,0)\) はともに\(y\)座標が0なので、グラフと\(x\)軸の交点です。
(例題)
3点、\((-2,0),(0,12),(3,0)\) を通る2次関数を求めよ。
(解答)
3点を代入して3つ式を作る方法でも解けますが、\(x\)軸との交点 \((-2,0),(3,0)\) が分かっているので \(y=a(x-α)(x-β)\) を利用します。
求める2次関数は、\(y=a(x+2)(x-3)\)とおける。
\((0,12)\)を代入して、\(12=-6a\) よって\(a=-2\)
したがって求める2次関数は \(y=-2(x+2)(x-3)\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。