関数に変数の定数がなく(固定された関数)で、定義域の片側だけが変数の場合の最大値最小値を見ていきましょう。
(問題)
\(a>0\)とし、関数 \(y=-x^2+2x\) (\(0≦x≦a\)) を考える。
(1)最大値を求めよ。 (2)最小値を求めよ。
関数自体は固定された具体的な関数です。定義域の片側は左端は固定されていて(\(x=0\))、右端は変数なので動きます。\(a\)を大きくしていくと定義域がどんどん広がっていくイメージです。最大最小値の候補は、頂点・両端ですが、軸と区域の位置関係で場合分けしていきます。
(解答)
\(y=-x^2+2x=-(x-1)^2+1\)
(1)
上に凸の2次関数なので、最大値は定義域内に軸を含むか(頂点が区域にある)どうかで変わってきます(区域内に頂点が無い場合は左端か右端になります)。\(a\)を0から徐々に増やしていくと、\(a<1\)では区域に頂点がないので左端と右端のうち大きいほうの右端、\(a≧1\)では区域に常に頂点があるので頂点の\(y\)座標が最大値になります。
上に凸の2次関数なので、最大値は定義域内に軸を含むか(頂点が区域にある)どうかで変わってきます(区域内に頂点が無い場合は左端か右端になります)。\(a\)を0から徐々に増やしていくと、\(a<1\)では区域に頂点がないので左端と右端のうち大きいほうの右端、\(a≧1\)では区域に常に頂点があるので頂点の\(y\)座標が最大値になります。
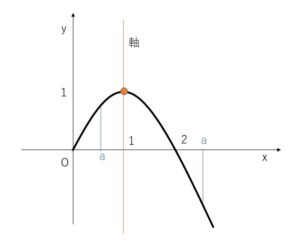
(ア) \(0<a<1\) のとき
最大値は \(x=a\)のときで
(最大値)\(=-a^2+2a\)
最大値は \(x=a\)のときで
(最大値)\(=-a^2+2a\)
(イ) \(a≧1\) のとき
最大値 \(x=1\)のときで
(最大値)\(=1\)
最大値 \(x=1\)のときで
(最大値)\(=1\)
(2)
上に凸のグラフなので最小値は左端か右端になります。左端か右端が同じ値になるとき(区域の中央に軸が位置する場合)の\(a\)は\(a=2\)のときなので、ここを境目に場合分けします。
上に凸のグラフなので最小値は左端か右端になります。左端か右端が同じ値になるとき(区域の中央に軸が位置する場合)の\(a\)は\(a=2\)のときなので、ここを境目に場合分けします。
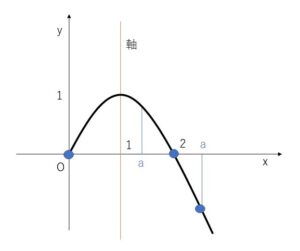
(ⅰ) \(0<a<2\)のとき
最小値は\(x=0\)のときで、
(最小値)\(=0\)
最小値は\(x=0\)のときで、
(最小値)\(=0\)
(ⅱ) \(a=2\)のとき
最小値は\(x=0,2\)のときで
(最小値)\(=0\)
最小値は\(x=0,2\)のときで
(最小値)\(=0\)
(ⅲ) \(a>2\)のとき
最小値は \(x=a\)のときで
(最小値)\(=-a^2+2a\)
最小値は \(x=a\)のときで
(最小値)\(=-a^2+2a\)
(ⅱ)を(ⅰ)(ⅲ) のどちらかに含ませてもよいです。\(a=2\)である(ⅱ)では 最小値が \(x=0\) または \(x=2=a\) のときの値なので、最小値が\(x=0\)の値である(ⅰ)、\(x=a\)の値である(ⅲ)のどちらに含ませても成り立つからです。
以上になります。お疲れさまでした。
ここまで読んで頂きありがとうございました。
ここまで読んで頂きありがとうございました。