2次関数の式に文字の定数があり、定義域は定数で固定された場合の最大最小値を考えていきます。やることは相変わらず軸と区域の位置関係で場合分けです。
(問題)
\(a\)を定数とする。2次関数 \(y=f(x)=x^2-2ax+2a^2\) (\(0≦x≦2\)) について
(1)最大値を求めよ (2)最小値を求めよ。
定義域は \(0≦x≦2\) で固定です。与えられた2次関数を平方完成すると、\(y=(x-a)^2+a^2\) で軸が文字定数となっています。\(a\)の値が変わると軸が動くイメージです。今回も軸と区域の位置関係で場合分けしていきます。
(解答)
(1)
与えられた2次関数は下に凸のグラフなので、最大値は左端か右端です。左端と右端の\(y\)座標が同じになるときは、区域の中央(\(x=1\))に軸が位置するときなので、\(a=1\)。これが場合分けの境目となります。
与えられた2次関数は下に凸のグラフなので、最大値は左端か右端です。左端と右端の\(y\)座標が同じになるときは、区域の中央(\(x=1\))に軸が位置するときなので、\(a=1\)。これが場合分けの境目となります。
(ア)\(a<1\)のとき
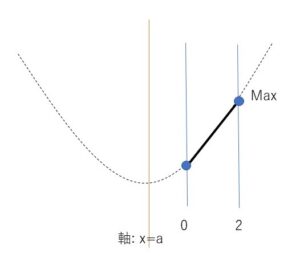
グラフより最大値は\(x=2\)のとき
\(f(2)=2a^2-4a+4\)
\(f(2)=2a^2-4a+4\)
(イ)\(a=1\)のとき
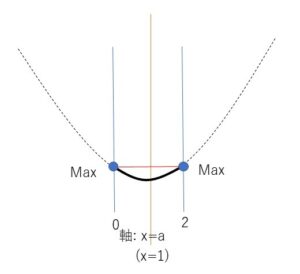

最大値は、\(x=0,2\)のとき
\(f(x)=x^2-2x+2\)から
\(f(0)=f(2)=2\)
\(f(0)=f(2)=2\)
(ウ)\(a>1\)のとき
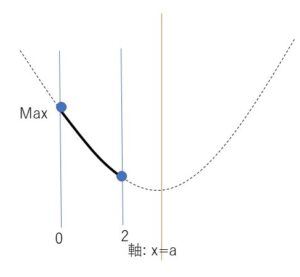
最大値は \(x=0\)のとき
\(f(0)=2a^2\)
\(f(0)=2a^2\)
(イ)を、(ア)か(ウ)に混ぜても構いません。
(2)
下に凸のグラフなので、最小値は区域に軸を含むか含まないかで場合分けです。区域に軸を含まない場合は、軸が区域の左側か右側かでも分けます。
下に凸のグラフなので、最小値は区域に軸を含むか含まないかで場合分けです。区域に軸を含まない場合は、軸が区域の左側か右側かでも分けます。
区域の左側に軸(区域の方がが右側) \(a<0\)・・・①
区域の中に軸 \(0≦a≦2\)・・・②
区域の右側に軸(区域の方が左側) \(a>2\)・・・③
区域の中に軸 \(0≦a≦2\)・・・②
区域の右側に軸(区域の方が左側) \(a>2\)・・・③
①\(a<0\)のとき
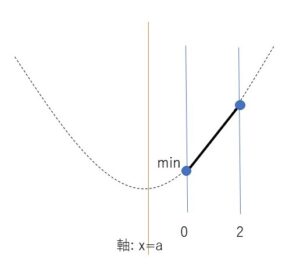
グラフより最小値は \(x=0\)のとき
\(f(0)=2a^2\)
\(f(0)=2a^2\)
②\(0≦a≦2\)のとき
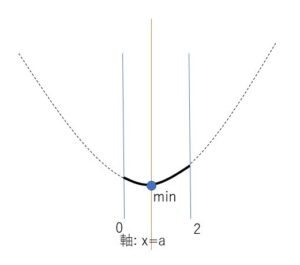
最小値は \(x=a\)のとき
\(f(a)=a^2\)
\(f(a)=a^2\)
③\(a>2\)のとき
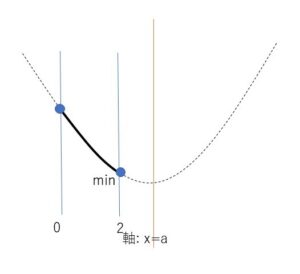
最小値は \(x=2\)のとき
\(f(2)=2a^2-4a+4\)
(1)と(2)を合わせたもの、つまり最大最小値を同時に考える場合は、境目が\(a=0,1,2\) なので (ⅰ)\(a<0\) (ⅱ)\(0≦a<1\) (ⅲ)\(a=1\) (ⅳ)\(1<a≦2\) (ⅴ)\(a>2\) の5パターンです。
以上になります。お疲れさまでした。
ここまで読んで頂きありがとうございました。