(問題)
次の不等式を解け
\(|x|+|x-2|<x+1\)
場合分けして式変形をしても解けますが、ここではグラフの位置関係から解を求めてみます。絶対値を含む1次関数に限らず、一般的な関数についてもグラフをかくことで不等式を解くことができます。
(解答)
左辺のグラフ(\(y=|x|+|x-2|\))と右辺のグラフ(\(y=x+1\))をそれぞれ書いてみます。
\(y=|x|+|x-2|\)について
①\(x<0\)のとき
\(y=-x-(x-2)=-2x+2\)
②\(0≦x<2\)のとき
\(y=x-(x-2)=2\)
③\(x≧2\)のとき
\(y=x+x-2=2x-2\)
\(y=-x-(x-2)=-2x+2\)
②\(0≦x<2\)のとき
\(y=x-(x-2)=2\)
③\(x≧2\)のとき
\(y=x+x-2=2x-2\)
よって\(y=|x|+|x-2|\) と \(y=x+1\) のグラフをまとめて図示すると以下の通りになる。
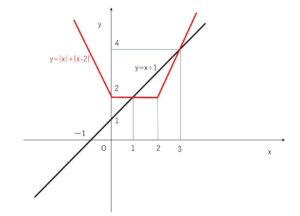
グラフの交点の\(x\)座標は、
②のとき
\(x+1=2\) から \(x=1\)
③のとき
\(x+1=2x-2\) から \(x=3\)
②のとき
\(x+1=2\) から \(x=1\)
③のとき
\(x+1=2x-2\) から \(x=3\)
したがって、グラフの位置関係から解は
\(1<x<3\)
\(1<x<3\)
\(|x|+|x-2|<x+1\)の解なので、左辺のほうが小さい、つまり\(y=|x|+|x-2|\) の赤色グラフのほうが下側にある\(x\)の範囲を探します。
以上になります。お疲れ様でした。
ここまで読んで下さりありがとうございました。
ここまで読んで下さりありがとうございました。