ある関数の定義域がさらにその関数である \(f(f(x))\) 型の関数について考えていきます。
\(=4x+3\) です。\(f=2□+1\)の□に\(2x+1\)を放り込んだ形です。
(問題)
\(x\) (\(0≦x≦1\)) の関数\(y=f(x)\)を次のように定義する。
\(
\begin{eqnarray}
f(x)
=
\begin{cases}
2x & (0≦x<\displaystyle\frac{1}{2})\\
2-2x & (\displaystyle\frac{1}{2}≦x≦1)
\end{cases}
\end{eqnarray}
\)
(1)\(y=f(x)\)のグラフをかけ。
(2)\(y=f(f(x))\)のグラフをかけ。
(1)グラフは以下のとおり。
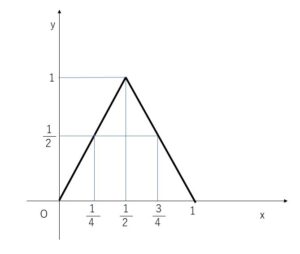
\(0≦x<\displaystyle\frac{1}{4}\) または \(\displaystyle\frac{3}{4}<x≦1\)
(b)\(\displaystyle\frac{1}{2}≦f(x)≦1\)のとき、(1)のグラフより
\(\displaystyle\frac{1}{4}≦x≦\displaystyle\frac{3}{4}\)なので、
もとの関数の場合分けの境目 \(x=\displaystyle\frac{1}{2}\)も含めて、4通りに分けます。(a)のときは外側の関数の形は\(2□\)で、(b)のときは外側の関数の形は\(2-2□\)となります。□に入るのはもちろん\(f(x)\)です。
①\(0≦x<\displaystyle\frac{1}{4}\)のとき
\(f(f(x))=2f(x)=2(2x)=4x\)
②\(\displaystyle\frac{1}{4}≦x<\displaystyle\frac{1}{2}\)のとき
\(f(f(x))=2-2f(x)=2-2(2x)=-4x+2\)
③\(\displaystyle\frac{1}{2}≦x≦\displaystyle\frac{3}{4}\)のとき
\(f(f(x))=2-2f(x)=2-2(2-2x)=4x-2\)
④\(\displaystyle\frac{3}{4}<x≦1\)のとき
\(f(f(x))=2f(x)=2(2-2x)=-4x+4\)
以上をグラフにすると以下の通りとなる。
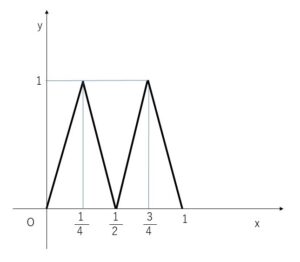
※ややこしい問題なのでじっくり考えてください。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。