2次方程式 \(ax^2+bx+c=0\) は、2次関数 \(y=ax^2+bx+c\) で \(y=0\) とおいたものなので、2次方程式 \(ax^2+bx+c=0\) が実数解をもつならば、2次関数 \(y=ax^2+bx+c\) で \(y=0\) となる実数\(x\)が存在することになるので、2次関数のグラフと\(x\)軸は交わることになります。2次方程式が実数解をもたない場合は、2次関数で、\(y=0\) となる実数\(x\)が存在しないため、グラフと\(x\)軸は交わらないことになります。つまり、2次関数が\(x\)軸と交わるかどうかは、\(y=0\) としたとき2次方程式が解をもつかどうかということと全く同じ議論になります。解の個数も考慮すると次のようにまとめることができます。
\(y=ax^2+bx+c\)について \(D=b^2-4ac\)とおくと
① \(D>0\) \(\leftrightarrow\) \(y=0\)の方程式が2つの実数解をもつ = グラフがx軸と2点で交わる
② \(D=0\) \(\leftrightarrow\) \(y=0\)の方程式がただ1つの実数解をもつ = グラフがx軸と1点で交わる
③ \(D<0\) \(\leftrightarrow\) \(y=0\)の方程式が実数解をもたない = グラフがx軸と交わらない
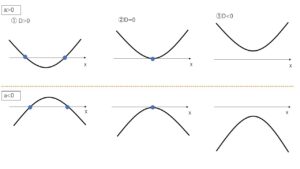
※結局、x軸と2次関数の共有点の問題は\(y=0\)としたときの2次方程式の実数解の個数の問題とほとんど同じになります。念のため少し例題をやっておきます。
(例題1)
次の2次関数のグラフと\(x\)軸の共有点はあるか。ある場合はその座標も求めよ。
(1) \(y=x^2-3x-4\)
(2) \(y=x^2+4x+5\)
(解答)
(1)
\(D=(-3)^2-4・1(-4)=25>0\) より2つの異なる共有点をもつ。
共有点は、\(x^2-3x-4=0\)を解くと \((x+1)(x-4)=0\)
よって \(x=-1,4\) ゆえに共有点の座標は
\((-1,0)\) \((4,0)\)
(2)
\(D=4^2-4・1・5=-4<0\) から共有点はない。
(例題2)
\(y=x^2-2(k-1)x-4k+9\) が\(x\)軸に接するように定数\(k\)の値を定めよ。またこのときの接点の座標も求めよ。
(解答)
\(\displaystyle\frac{D}{4}=(k-1)^2-1・(-4k+9)=k^2+2k-8=0\) より
\((k+4)(k-2)=0\) よって
\(k=-4,2\)
①\(k=-4\)のとき 方程式\(y=0\)は
\(x^2+10x+25=0\) となるので \(x=-5\)
②\(k=2\)のとき 方程式\(y=0\)は
\(x^2-2x+1=0\) となるので \(x=1\)
以上から
\(k=-4\) のとき 接点 \((-5,0)\)
\(k=2\) のとき 接点 \((1,0)\)
(例題3)
\(y=x^2-4x+k\) と\(x\)軸の共有点の個数を調べよ。
(解答)
\(\displaystyle\frac{D}{4}=4-k\)
①\(D>0\) つまり \(4-k>0\) のとき \(k<4\)
②\(D=0\) つまり \(4-k=0\) のとき \(k=4\)
③\(D<0\) つまり \(4-k<0\) のとき \(k>4\)
以上から共有点の個数は
\(k<4\) のとき 2個
\(k=4\) のとき 1個
\(k>4\) のとき 0個
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。