→(6-3)実数解の個数とグラフとx軸の共有点 では2次関数と\(x\)軸の共有点について考えましたが、今回は2次関数と直線について考えます。
・放物線と直線
放物線 \(y=ax^2+bx+c\) と直線 \(y=mx+n\) の共有点を考えるとき、\(y\)座標が等しいことから、2式を連立します。\(y\)を消去した式は \(ax^2+bx+c=mx+n\) となり整理すると、
\(ax^2+(b-m)x+c-n=0\)・・・① となります。
①は2次方程式なので、判別式\(D\)の値で解の個数が変化しますね。\(D>0\)の場合には①が2つの異なる実数解をもつことと、①の解\(x\)は共有点の\(x\)座標を表すことから、異なる2点で放物線と直線は交わることになります。\(D=0\) \(D<0\)も同様に考えると以下のようにまとめることができます。
①式の判別式を\(D\)とする。
(1)\(D>0\) \(\leftrightarrow\) ①が異なる2つの実数解をもつ=異なる2点で交わる
(2)\(D>0\) \(\leftrightarrow\) ①がただ1つの実数解(重解)をもつ=1点で交わる
(3)\(D>0\) \(\leftrightarrow\) ①が実数解をもたない=共有点をもたない
(1)\(D>0\) \(\leftrightarrow\) ①が異なる2つの実数解をもつ=異なる2点で交わる
(2)\(D>0\) \(\leftrightarrow\) ①がただ1つの実数解(重解)をもつ=1点で交わる
(3)\(D>0\) \(\leftrightarrow\) ①が実数解をもたない=共有点をもたない

(2)では方程式①の解が重解となるので、放物線と直線は接点で接することになります。
今回も「重解=接する」と覚えてください。(微分の知識があれば導くことができます。)
(例題1)
次の放物線と直線の共有点を調べよ。
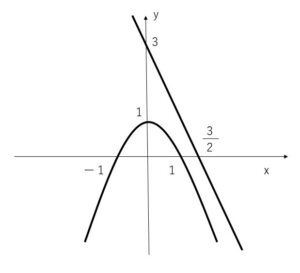
\(y=-x^2+1\), \(y=-2x+3\)
次の放物線と直線の共有点を調べよ。
\(y=-x^2+1\), \(y=-2x+3\)
(解答)
\(y\)を消去すると、
\(-x^2+1=-2x+3\)から
\(x^2-2x+2=0\)・・・①
①の判別式 \(D=4-8=-4<0\)より
方程式①は解をもたない。よって共有点はない。
\(y\)を消去すると、
\(-x^2+1=-2x+3\)から
\(x^2-2x+2=0\)・・・①
①の判別式 \(D=4-8=-4<0\)より
方程式①は解をもたない。よって共有点はない。
(例題2)
\(k\)を定数とする。関数 \(y=-x^2\) のグラフと直線 \(y=-2x+k\)との共有点の個数を調べよ。
\(k\)を定数とする。関数 \(y=-x^2\) のグラフと直線 \(y=-2x+k\)との共有点の個数を調べよ。
(解答)
2式から\(y\)を消去して
\(-x^2=-2x+k\) 整理すると
\(x^2-2x+k=0\)・・・①
①について \(\displaystyle\frac{D}{4}=1-k\)
2式から\(y\)を消去して
\(-x^2=-2x+k\) 整理すると
\(x^2-2x+k=0\)・・・①
①について \(\displaystyle\frac{D}{4}=1-k\)
(1)\(D>0\)のとき
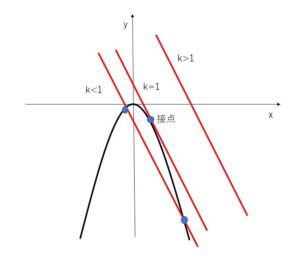
\(1-k>0\) つまり \(k<1\)のとき ①は異なる2つの実数解をもち、共有点は2個
\(1-k>0\) つまり \(k<1\)のとき ①は異なる2つの実数解をもち、共有点は2個
(2)\(D=0\)のとき
\(1-k=0\) つまり \(k=1\)のとき ①は重解をもち、共有点は1個
\(1-k=0\) つまり \(k=1\)のとき ①は重解をもち、共有点は1個
(3)\(D<0\)のとき
\(1-k<0\) つまり \(k>1\)のとき ①は実数解をもたないため、共有点は0個
\(1-k<0\) つまり \(k>1\)のとき ①は実数解をもたないため、共有点は0個
以上から
\(k<1\)のとき2個、\(k=1\)のとき1個、\(k>1\)のとき0個
\(k<1\)のとき2個、\(k=1\)のとき1個、\(k>1\)のとき0個
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。