前回 (→(8-3))紹介した、2次方程式の解の存在範囲についての性質を利用して、解と2次方程式の係数の大小を調べてみます。
(問題)
\(a<b<c\) のとき、\(x\)に関する方程式 \(2(x-b)(x-c)-(x-a)^2=0\) は2つの解をもつことを示せ。また、その解を\(α,β\)(\(α<β)\)とするとき、\(α,β\)と定数\(a,b,c\)の大小関係を示せ。
(解答)
\(f(x)=2(x-b)(x-c)-(x-a)^2\)とおくと
\(f(a)=2(a-b)(a-c)>0\) (\(∵a-b<0,a-c<0\))
\(f(b)=-(b-a)^2<0\)
\(f(c)=-(c-a)^2<0\)
また、\(f(x)\)の2次の係数は1で、\(y=f(x)\)のグラフは下に凸の放物線。
よって\(c\)より大きい値\(d\)で\(f(d)>0\)となるものが存在する。
したがって\(y=f(x)\)のグラフは、\(a<x<b\) と \(c<x<d\) の範囲で\(x\)軸と交わるから、方程式\(f(x)=0\)は2つの解をもつ。また以上のことからグラフを描くと以下のようになる。
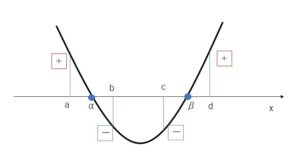
グラフより、\(a<α<b<c<β\) となる。
2次の係数が1になるのが分からない人は展開してみてください。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。