2次方程式が実数解をもち、その解のうち少なくとも1つがある区間にある条件を考えます。少なくとも1つがある区間にあるということは、2次方程式の2解両方がある区間に存在するか、1つだけがある区間に存在するかの2パターンの場合があるので、→(8-5)ある区間に2つの解・→(8-6)ある区間にただ1つの解 を合わせた融合問題と考えればそれほど難しくはりません。
(問題)
方程式 \(x^2+(a+2)x-a+1=0\) が \(-2<x<0\) の範囲に少なくとも1つの実数解をもつような定数\(a\)の値の範囲を求めよ。
(解答)
\(f(x)=x^2+(a+2)x-a+1\) とする。
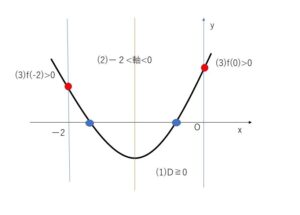
(A)2つの解(重解を含む)がともに、\(-2<x<0\) の範囲にある条件は
(1)判別式 \(D≧0\)
(2)軸について \(-2<-\displaystyle\frac{a+2}{2}<0\)
(3)端点について \(f(-2)>0\) \(f(0)>0\)
(1)より \(D=(a+2)^2-4(-a+1)=a^2+8a=a(a+8)≧0\)
よって \(a≦-8,a≧0\)・・・①
(2)より \(-2<a<2\)・・・②
(3)より \(f(-2)=-3a+1>0\) より \(a<\displaystyle\frac{1}{3}\)・・・③
\(f(0)=-a+1>0\) より \(a<1\)・・・④
①~④の共通部分を求めると、 \(0≦a<\displaystyle\frac{1}{3}\)
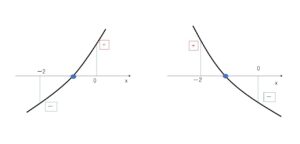
(B)解の1つが \(-2<x<0\)、もう1つの解が \(x<-2\) または \(x>0\)にある条件は \(f(-2)f(0)<0\)
よって \((-3a+1)(-a+1)<0\) から \((3a-1)(a-1)<0\)
ゆえに \(\displaystyle\frac{1}{3}<a<1\)
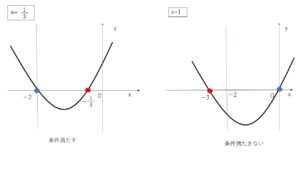
(C)解の1つが \(x=-2,0\) のときは \(f(0)f(-2)=0\)から
\((-3a+1)(-a+1)=0\) \(a=\displaystyle\frac{1}{3},1\)
\(a=\displaystyle\frac{1}{3}\) のとき 方程式は \(x^2+\displaystyle\frac{7}{3}x+\displaystyle\frac{2}{3}=0\) となり \((x+2)(x+\displaystyle\frac{1}{3})=0\) から、もう1つの解は \(x=-\displaystyle\frac{1}{3}\) よって条件を満たす。
\(a=1\)のとき 方程式は \(x^2+3x=0\) となり \(x(x+3)=0\)から、もう1つの解は \(x=-3\) よって条件を満たさない。
以上(A)~(C)より \(0≦a<1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。