絶対値を含む2次関数のグラフについて考えていきます。
(例題)次のグラフをかけ
(1) \(y=|x^2-4x+3|\) (2) \(y=|x^2-3x|-x+2\)
絶対値をはずすために、絶対値の中身の正負で場合わけします。
(1)
\(x^2-4x+3=(x-1)(x-3)\) より
①\(x≦1\) または \(x≧3\) のとき
\(y=x^2-4x+3=(x-2)^2-1\)
② \(1<x<3\) のとき
\(y=-(x^2-4x+3)=-(x-2)^2+1\)
①②からグラフは以下の図となる。
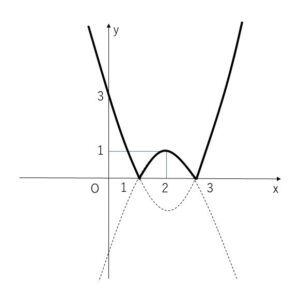
\(y=|f(x)|\)において、\(f(x)≧0\) のとき \(y=f(x)\)、\(f(x)<0\) のとき \(y=-f(x)\) なので、\(y=|f(x)|\)のグラフを書くときは、まず\(y=f(x)\)を書いて、\(f(x)≧0\)の部分はそのままで、\(f(x)<0\)の部分は\(x\)軸について対称に折り返せばよいことになります。
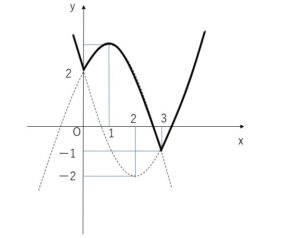
(2) \(y=|x^2-3x|-x+2\)
\(x^2-3x=x(x-3)\) より
①\(x≦0\) または \(x≧3\)のとき
\(y=(x^2-3x)-x+2=x^2-4x+2\)
\(=(x-2)^2-2\)
②\(0<x<3\) のとき
\(y=-(x^2-3x)-x+2=-x^2+2x+2\)
\(=-(x-1)^2+3\)
①②よりグラフは下図となる。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。