\((a+b)^n\) を展開すると、どのような結果になるか学んでいきます。
・二項定理
\((a+b)^4\)を展開公式を利用して計算すると
\((a+b)^4\)
\(=(a+b)^3(a+b)\)
\(=(a^3+3a^2b+3ab^2+b^3)\)\((a+b)\)
\(=a^4+3a^3b\)\(+3a^2b^2+ab^3\)
\(+a^3b+3a^2b^2\)\(+3ab^3+b^4\)
\(=\)\(a^4+4a^3b+6a^2b^2\)\(+4ab^3+b^4\)
となりますが、もうすこし楽に計算できる別の方法(二項定理)があります。
\((a+b)^4=(a+b)(a+b)\)\((a+b)(a+b)\)
なので、例えば\(a^3b\)の項は、4箇所の\((a+b)\)から、\(a\)を3つ\(b\)を1つ選んで掛けあわせたものからできています。
\(a\)を3つ、\(b\)を1つ選ぶ方法は、4つの\((a+b)\)から\(b\)を1つ選ぶ方法(もしくは\(a\)を3つ選ぶ方法)あるので、\(a^3b\)の係数は\({}_4\mathrm{C}_1\)となります。
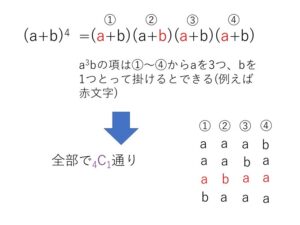
なお、\({}_4\mathrm{C}_1\)は、\(a\)3つ\(b\)1つを並べる方法(同じものを含む順列)の総数です。
以上のことを一般化すると
\((a+b)^n\) (\(n\)は自然数)を展開すると、\(a,b\)についての\(n\)次の項
\(a^n,a^{n-1}b,a^{n-2}b^2,・・・\)\(,a^{n-r}b^{r},・・・\)\(,ab^{n-1},b^{n}\) (\(a,b\)の指数の和は\(n\)であることに注意)
があらわれ、それぞれの係数は \(n\)個の\((a+b)\)から\(b\)を選ぶ方法を考えて
\({}_n\mathrm{C}_0,{}_n\mathrm{C}_1,{}_n\mathrm{C}_2,・・・\)\(,{}_n\mathrm{C}_r,・・・\)\(,{}_n\mathrm{C}_{n-1},{}_n\mathrm{C}_{n}\)
となり、次の定理が成り立ちます。
\((a+b)^n\)
\(={}_n\mathrm{C}_0a^{n}+{}_n\mathrm{C}_1a^{n-1}b+{}_n\mathrm{C}_2a^{n-2}b^{2}+・・・\)
\(+\)\({}_n\mathrm{C}_ra^{n-r}b^{r}\)\(+・・・+{}_n\mathrm{C}_{n-1}ab^{n-1}+{}_n\mathrm{C}_{n}b^{n}\)
この定理を二項定理、第\(r+1\)項 \({}_n\mathrm{C}_{r}a^{n-r}b^{r}\) を一般項、\({}_n\mathrm{C}_{r}\)を二項係数とよびます。
(例題)次の式を展開せよ。
(1)\((2a-3b)^5\)
(2)\((x+\displaystyle\frac{1}{x})^4\)
(解答)
(1)
\((2a-3b)^5\)
\(={}_5\mathrm{C}_0(2a)^5+{}_5\mathrm{C}_1(2a)^4(-3b)\)\(+{}_5\mathrm{C}_2(2a)^3(-3b)^2\)\(+{}_5\mathrm{C}_3(2a)^2(-3b)^3\)
\(+{}_5\mathrm{C}_4(2a)(-3b)^4+{}_5\mathrm{C}_5(-3b)^5\)
\(=\)\(32a^5-240a^4b+720a^3b^2\)\(-1080a^2b^3\)\(+810ab^4\)\(-243b^5\)
(2)
\((x+\displaystyle\frac{1}{x})^4\)
\(={}_4\mathrm{C}_0x^4+{}_4\mathrm{C}_1x^3\displaystyle\frac{1}{x}\)\(+{}_4\mathrm{C}_2x^2(\displaystyle\frac{1}{x})^2\)\(+{}_4\mathrm{C}_3x(\displaystyle\frac{1}{x})^3\)\(+{}_4\mathrm{C}_4(\displaystyle\frac{1}{x})^4\)
\(=\)\(x^4+4x^2+6+\)\(\displaystyle\frac{4}{x^2}+\displaystyle\frac{1}{x^4}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。