これから三角比について学んでいきます。
三角比とは直角三角形の2辺の比のことです。何も特徴のないただの三角形ではなく直角三角形の辺の比です。角\(C\)が直角である直角三角形\(ABC\)について図のように辺の長さを\(a,b,c\)とおきます。2辺の比を考えるので、組み合わせは \(a\)と\(c\), \(b\)と\(c\), \(a\)と\(b\) の3通りです。辺の比を表すには、例えば\(a\)と\(c\)では\(a:c\)と表すこともできますが、三角比では分数の形で表します。
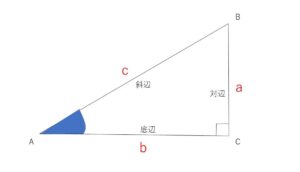
さて、分数の形に表すときに先ほどの3通りの組み合わせのそれぞれでどちらを分母にするかを考えると全部で6通りの場合が考えられますが、三角比では主にそのうちの3通りについて考えていきます。対辺\(a\)と斜辺\(c\)では分母は\(c\)の\(\displaystyle\frac{a}{c}\)、底辺\(b\)と斜辺\(c\)では分母は\(c\)の\(\displaystyle\frac{b}{c}\)、対辺\(a\)と底辺\(b\)では分母は\(b\)の\(\displaystyle\frac{a}{b}\)です。これらにはすべて名前がついていて、順に角\(A\)の正弦(サイン)、余弦(コサイン)、正接(タンジェント)といい、角\(A\)の大きさを\(A\)とすれば、\(sinA\)、\(cosA\)、\(tanA\)と表されます。
\(sinA=\displaystyle\frac{a}{c}=\displaystyle\frac{対辺}{斜辺}\)
\(cosA=\displaystyle\frac{b}{c}=\displaystyle\frac{底辺}{斜辺}\)
\(tanA=\displaystyle\frac{a}{b}=\displaystyle\frac{対辺}{底辺}\)
覚え方は \(sin,cos,tan\) の頭文字を筆記体にして三角形の図と対応させます。
(→の向きでで分母→分子の順)
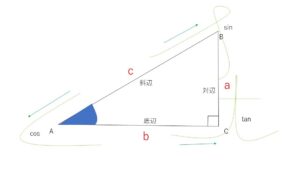
三角比で角(直角三角形の定義では鋭角)について考えるのはこのためです。
\(secA=\displaystyle\frac{c}{b}=\displaystyle\frac{1}{cosA}\)
\(cosecA=\displaystyle\frac{c}{a}=\displaystyle\frac{1}{sinA}\)
\(cotA=\displaystyle\frac{b}{a}=\displaystyle\frac{1}{tanA}\)
です。
\(30°,45°,60°\)の三角比は正三角形と正方形をそれぞれ半分にした図形から具体的な値をもとめることができます。
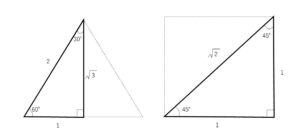
\(sin30°=\displaystyle\frac{1}{2}\), \(cos30°=\displaystyle\frac{\sqrt{3}}{2}\), \(tan30°=\displaystyle\frac{1}{\sqrt{3}}\)
\(sin45°=\displaystyle\frac{1}{\sqrt{2}}\), \(cos45°=\displaystyle\frac{1}{\sqrt{2}}\), \(tan45°=1\)
\(sin60°=\displaystyle\frac{\sqrt{3}}{2}\), \(cos60°=\displaystyle\frac{1}{2}\), \(tan60°=\sqrt{3}\)
忘れたら図を描いて求めてください。
(例題)
次の図の直角三角形\(ABC\)で、\(sinA,cosA,tanA\)の値を求めよ。
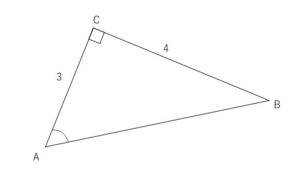
(解答)
三平方の定理より \(AB=\sqrt{16+9}=\sqrt{25}=5\)
よって \(sinA=\displaystyle\frac{4}{5}\), \(cosA=\displaystyle\frac{3}{5}\), \(tanA=\displaystyle\frac{4}{3}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。