角度\(θ\)が、\(0°≦θ≦180°\)の範囲で動くとき、\(\sinθ,\cosθ,\tanθ\)はどのような値をとりうるでしょうか。
・三角比の値の範囲
三角比の値は、円の半径の大きさによらず角度だけで決まるので、半径1の単位円について考えていきます。図のように、\(\angle AOP=θ\) となるような点\(P\)が単位円の周上にあるとき、三角比の定義より
\(\sinθ=\displaystyle\frac{y}{1}=y\) \(\cosθ=\displaystyle\frac{x}{1}=x\)
となります。つまり\(\sinθ\)は点\(P\)の\(y\)座標、\(\cosθ\)は\(x\)座標となります。
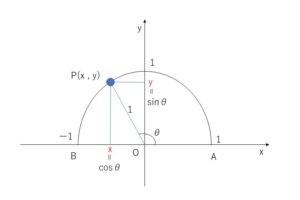
角度\(θ\)が、\(0°≦θ≦180°\)の範囲で変化するとき、点\(P\)は単位円の周上を\(A\)から\(B\)に動くため、\(x,y\)のとりうる値の範囲は、 \(-1≦x≦1\) , \(0≦y≦1\) となります。よって \(\sinθ,\cosθ\) のとりうる値の範囲は
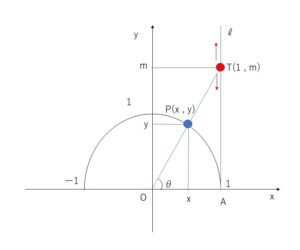
\(\tanθ=\displaystyle\frac{y}{x}=\displaystyle\frac{m}{1}\) つまり \(\tanθ=m\) (\(θ≠90°\))
この範囲で\(θ\)を\(0°→90°\)と変化させると、\(T\)は\(A\)から直線\(l\)上を上方向に動き、\(m\)は\(0\)と正の数全体の値をとる。
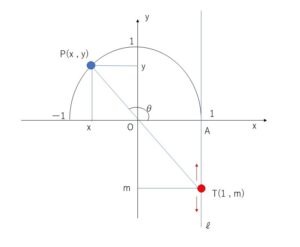
この範囲で\(θ\)を\(90°→180°\)と変化させると、\(T\)は直線\(l\)上を下方から\(A\)まで動き、\(m\)は負の数全体と\(0\)の値をとる。
\(-1≦\cosθ≦1\) , \(0≦\sinθ≦1\)
\(\tanθ\)は任意の値をとる。ただし、\(\tan90°\)は定義されない。
・三角比の値の符号
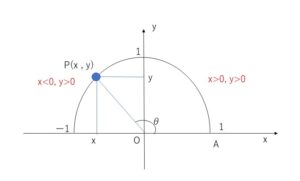
単位円を考えると、\(\sinθ\)は座標平面上で円周上の点\(P\)の\(y\)座標、\(\cosθ\)は\(x\)座標なので、\(点P\)が第一象限にある場合、つまり\(0°<θ<90°\)の場合、\(x>0,y>0\) より \(\sinθ>0,\cosθ>0\) となります。\(\tanθ\)についても\(\tanθ=\displaystyle\frac{y}{x}\)より、\(\tanθ>0\)となります。
\(点P\)が第二象限にある場合、つまり\(90°<θ<180°\)の場合、\(x<0,y>0\) より \(\sinθ>0,\cosθ<0\) で、\(\tanθ\)は\(x,y\)が異符号だから、\(\tanθ<0\) です。
\(θ=0°,90°,180°\)のときもあわせてまとめると次のようになります。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。