\(90°-θ\)、\(90°+θ\)、\(180°-θ\)の三角比は、\(\sinθ,\cosθ,\tanθ\)を使ってどのように表されるのでしょうか。
・\(90°-θ\)の三角比
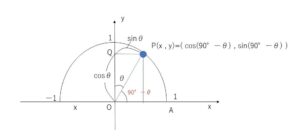
\(0°≦θ≦90°\)で、図のように単位円の周上に\(\angle AOP=90°-θ\)となるように、点\(P(x,y)\)をとる。\(P\)から\(y\)軸に下した垂線の足を\(Q\)とすると、\(\angle POQ=θ\) となるので、
\(OQ=\cosθ\) , \(QP=\sinθ\) よって
\(\sin(90°-θ)=y=OQ=\cosθ\)
\(\cos(90°-θ)=x=QP=\sinθ\)
\(θ≠0°,90°\)のとき
\(\tan(90°-θ)=\displaystyle\frac{y}{x}=\displaystyle\frac{OQ}{QP}=\displaystyle\frac{1}{\displaystyle\frac{QP}{OQ}}=\displaystyle\frac{1}{\tanθ}\)
\(\sin(90°-θ)=\cosθ\)
\(\cos(90°-θ)=\sinθ\)
\(\tan(90°-θ)=\displaystyle\frac{1}{\tanθ}\) (\(θ≠0°,90°\))。
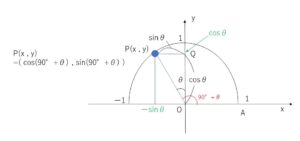
\(0°≦θ≦90°\)で、図のように単位円の周上に\(\angle AOP=90°+θ\)となるように、点\(P(x,y)\)をとる。\(P\)から\(y\)軸に下した垂線の足を\(Q\)とすると、\(\angle POQ=θ\) となるので、
\(OQ=\cosθ\) , \(QP=\sinθ\)
\(P\)の\(x\)座標は0以下の値であることに注意すると、
\(\sin(90°+θ)=y=OQ=\cosθ\)
\(\cos(90°+θ)=x=-QP=-\sinθ\)
\(θ≠0°,90°\)のとき
\(\tan(90°+θ)=\displaystyle\frac{y}{x}=\displaystyle\frac{OQ}{-QP}=-\displaystyle\frac{1}{\displaystyle\frac{QP}{OQ}}=-\displaystyle\frac{1}{\tanθ}\)
\(\sin(90°+θ)=\cosθ\)
\(\cos(90°+θ)=-\sinθ\)
\(\tan(90°+θ)=-\displaystyle\frac{1}{\tanθ}\) (\(θ≠0°,90°\))
・\(180°-θ\)の三角比
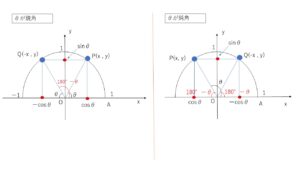
\(0°≦θ≦180°\)で図のように、単位円の周上に\(\angle AOP=θ\)となるように、点\(P(x,y)\)をとる。このとき、\(y\)座標に関して対称な点\(Q(-x,y)\)も半円の円周上にあり、\(\angle AOQ=180°-θ\) なので、\(Q(\cos(180°-θ),\sin(180°-θ))\)である。
\(\sinθ=y\) , \(\cosθ=x\) , \(\tanθ=\displaystyle\frac{y}{x}\) だから
\(\sin(180°-θ)=y=\sinθ\)
\(\cos(180°-θ)=-x=-\cosθ\)
\(\tan(180°-θ)=\displaystyle\frac{y}{-x}=-\tanθ\)
\(\sin(180°-θ)=\sinθ\)
\(\cos(180°-θ)=-\cosθ\)
\(\tan(180°-θ)=-\tanθ\)
\(\sin80°+\cos110°+\sin160°+\cos170°\)
(与式)\(=\sin(90°-10°)+\cos(90°+20°)+\sin(180°-20°)+\cos(180°-10°)\)
\(=\cos10°-\sin20°+\sin20°-\cos10°=\)\(0\)
(例題2)次の式を簡単にせよ。
\(2\tan145°\tan125°+\tan155°\tan115°\)
(解答)
(与式)\(=2\tan(180°-35°)\tan(90°+35°)+\tan(180°-25°)\tan(90°+25°)\)
\(=2(-\tan35°)(-\displaystyle\frac{1}{\tan35°})+(-\tan25°)(-\displaystyle\frac{1}{\tan25°})\)
\(=2+1=\)\(3\)
三角比の分野は公式を覚えたり使いこなすのに慣れが必要です。
練習を積み重ねましょう。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。