2次の三角方程式について見ていきます。三角比の相互関係、三角比のとりうる値の範囲に注意します。
(問題1)
\(0°≦θ≦180°\) とする。次の等式を満たす\(θ\)の値を求めよ。
\(2\cos^2θ+11\sinθ-7=0\)
\(\sin\)と\(\cos\)の両方が混ざっているので、片方に統一します。
(解答)
\(\cos^2θ=1-\sin^2θ\) を与式に代入して、
\(2(1-\sin^2θ)+11\sinθ-7=0\)
整理して
\(2\sin^2θ-11\sinθ+5=0\)
\((2\sinθ-1)(\sinθ-5)=0\) となり
\(\sinθ=\displaystyle\frac{1}{2},5\)
\(\cos^2θ=1-\sin^2θ\) を与式に代入して、
\(2(1-\sin^2θ)+11\sinθ-7=0\)
整理して
\(2\sin^2θ-11\sinθ+5=0\)
\((2\sinθ-1)(\sinθ-5)=0\) となり
\(\sinθ=\displaystyle\frac{1}{2},5\)
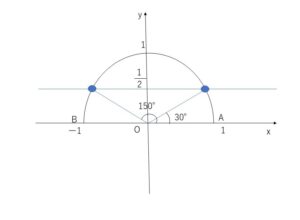
\(0°≦θ≦180°\) のとき \(0≦\sinθ≦1\)だから
\(\sinθ=\displaystyle\frac{1}{2}\)
\(\sinθ=\displaystyle\frac{1}{2}\)
したがって \(θ=30°,150°\)
(問題2)
\(0°≦θ≦180°\) とする。次の等式を満たす\(θ\)の値を求めよ。
\(\sqrt{2}\sinθ=\tanθ\)
\(0°≦θ≦180°\) とする。次の等式を満たす\(θ\)の値を求めよ。
\(\sqrt{2}\sinθ=\tanθ\)
\(\tanθ=\displaystyle\frac{\sinθ}{\cosθ}\)を利用して、ひとまず与式を\(\sinθ\)と\(\cosθ\)の式にします。
(解答)
\(θ≠90°\)で 与式は
\(θ≠90°\)で 与式は
\(\sqrt{2}\sinθ=\displaystyle\frac{\sinθ}{\cosθ}\) であり、両辺に\(\cosθ\)を掛けて
\(\sqrt{2}\sinθ\cosθ=\sinθ\)
よって、\(\sinθ(\sqrt{2}\cosθ-1)=0\) であるから
\(\sinθ=0\) または \(\cosθ=\displaystyle\frac{1}{\sqrt{2}}\)
\(\sqrt{2}\sinθ\cosθ=\sinθ\)
よって、\(\sinθ(\sqrt{2}\cosθ-1)=0\) であるから
\(\sinθ=0\) または \(\cosθ=\displaystyle\frac{1}{\sqrt{2}}\)
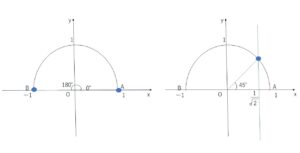
したがって \(θ=0°,45°,180°\) (\(θ≠90°\)を満たす)
以上です。お疲れさまでした。
ここまで見て頂きありがとうございました。