・三角形の面積
三角形の面積は (底辺)×(高さ)÷2 で求められるのは知っていると思いますが、三角比を用いた三角形の面積の公式を紹介します。
\(△ABC\)の面積を\(S\)とし、図ように底辺\(AB\)に対する高さを\(h\)とします。
\(h=b\sin A\) なので、\(S=\displaystyle\frac{1}{2}ch=\displaystyle\frac{1}{2}bc\sin A\) となります。
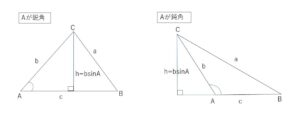
同様に、\(S=\displaystyle\frac{1}{2}ca\sin B=\displaystyle\frac{1}{2}ab\sin C\) が成り立ちます。
\(△ABC\)の面積\(S\)は
\(S=\displaystyle\frac{1}{2}bc\sin A=\displaystyle\frac{1}{2}ca\sin B=\displaystyle\frac{1}{2}ab\sin C\)
\(S=\displaystyle\frac{1}{2}\)×(挟む2辺)×\(\sin\)(挟まれる角)です。
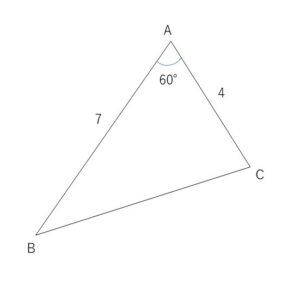
(例題1)次の三角形\(ABC\)の面積を求めよ。
\(b=4\), \(c=7\), \(A=60°\)
\(b=4\), \(c=7\), \(A=60°\)
(解答)
\(S=\displaystyle\frac{1}{2}・4・7\sin60°=\displaystyle\frac{1}{2}・4・7・\displaystyle\frac{\sqrt{3}}{2}=\)\(7\sqrt{3}\)
\(S=\displaystyle\frac{1}{2}・4・7\sin60°=\displaystyle\frac{1}{2}・4・7・\displaystyle\frac{\sqrt{3}}{2}=\)\(7\sqrt{3}\)
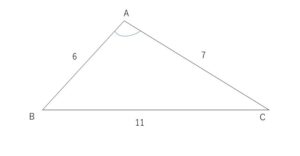
(例題2)次の三角形\(ABC\)の面積を求めよ。
\(a=11,b=7,c=6\)
\(a=11,b=7,c=6\)
\(\sin A\)を求めるために、余弦定理から\(\cos A\)をまず求めます。
(解答)
余弦定理より
\(\cos A=\displaystyle\frac{7^2+6^2-11^2}{2・7・6}=-\displaystyle\frac{3}{7}\)
よって、\(0°<A<180°\)より \(\sin A>0\) だから
\(\sin A=\sqrt{1-(\displaystyle\frac{3}{7})^2}=\displaystyle\frac{2\sqrt{10}}{7}\)
余弦定理より
\(\cos A=\displaystyle\frac{7^2+6^2-11^2}{2・7・6}=-\displaystyle\frac{3}{7}\)
よって、\(0°<A<180°\)より \(\sin A>0\) だから
\(\sin A=\sqrt{1-(\displaystyle\frac{3}{7})^2}=\displaystyle\frac{2\sqrt{10}}{7}\)
したがって、\(S=\displaystyle\frac{1}{2}・7・6\sin A=\displaystyle\frac{1}{2}・7・6・\displaystyle\frac{2\sqrt{10}}{7}=\)\(6\sqrt{10}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
ここまで見て頂きありがとうございました。