三角形の外接円・内接円の半径を求めていきます。
(問題)
\(△ABC\)において、\(AB=9,BC=17,CA=10\) のとき次の値をそれぞれ求めよ。
(1)外接円の半径\(R\)
(2)内接円の半径\(r\)
(1)外接円の半径なので、正弦定理を利用します。まずは\(\cos A\)を余弦定理で求めて、そこから\(\sin A\)を求めます。
(解答)
(1)
(1)
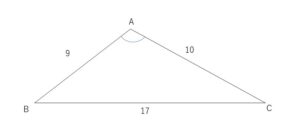
余弦定理より
\(\cos A=\displaystyle\frac{9^2+10^2-17^2}{2・9・10}=-\displaystyle\frac{3}{5}\)
\(0°<A<180°\) より \(\sin A>0\) だから
\(\sin A=\sqrt{1-(\displaystyle\frac{3}{5})^2}=\displaystyle\frac{4}{5}\)
\(\cos A=\displaystyle\frac{9^2+10^2-17^2}{2・9・10}=-\displaystyle\frac{3}{5}\)
\(0°<A<180°\) より \(\sin A>0\) だから
\(\sin A=\sqrt{1-(\displaystyle\frac{3}{5})^2}=\displaystyle\frac{4}{5}\)
よって正弦定理より
\(2R=\displaystyle\frac{BC}{\sin A}\) だから
\(R=\displaystyle\frac{17}{2}÷\displaystyle\frac{4}{5}=\)\(\displaystyle\frac{85}{8}\)
\(2R=\displaystyle\frac{BC}{\sin A}\) だから
\(R=\displaystyle\frac{17}{2}÷\displaystyle\frac{4}{5}=\)\(\displaystyle\frac{85}{8}\)
(2)
内接円は各辺\(AB,BC,CA\)に接する円です。内接円の中心を\(I\)とし、\(I\)と各頂点\(A,B,C\)を結び三角形を3つ作ります。これらの三角形は底辺をそれぞれ\(AB,BC,CA\)とすると、\(I\)と各接点を結ぶと各辺と垂直に交わるので、高さは3つとも内接円の半径\(r\)となります。
全体の三角形\(ABC\)の面積をまず求め、分割した3つの三角形の面積を\(r\)で表すことで、「\(△ABC=\)(3つの三角形の面積の和)」として\(r\)の方程式を作ります。
全体の三角形\(ABC\)の面積をまず求め、分割した3つの三角形の面積を\(r\)で表すことで、「\(△ABC=\)(3つの三角形の面積の和)」として\(r\)の方程式を作ります。
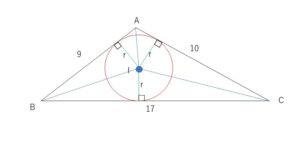
三角形\(ABC\)の内接円の中心を\(I\)とすると
\(△ABC=△IBC+△ICA+△IAB\)
\(△ABC=△IBC+△ICA+△IAB\)
ここで、
\(△ABC=\displaystyle\frac{1}{2}・9・10・\sin A=9・5・\displaystyle\frac{4}{5}=36\) だから
\(△ABC=\displaystyle\frac{1}{2}・9・10・\sin A=9・5・\displaystyle\frac{4}{5}=36\) だから
\(36=\displaystyle\frac{1}{2}・17・r+\displaystyle\frac{1}{2}・10・r+\displaystyle\frac{1}{2}・9・r\)
\(36=\displaystyle\frac{r}{2}(17+10+9)\) より
\(r=2\)
以上です。お疲れ様でした。
ここまで読んで頂きありがとうございました。