今回は、正四面体ではない四面体の体積について考えていきます。正四面体ではないですが、特徴のある四面体を扱っていきます。
(例題1)
四面体\(ABCD\)において、\(AB=3,BC=\sqrt{13},CA=4,DA=DB=DC=3\) とし、頂点\(D\)から\(△ABC\)に垂線\(DH\)を下ろす。このとき線分\(DH\)の長さと四面体\(ABCD\)の体積を求めよ。
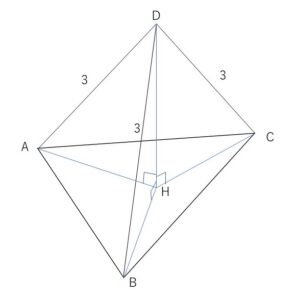
\(0°<\angle BAC<180°\) だから、\(\angle BAC=60°\)である。
よって、\(△ABC\)の外接円の半径を\(R\)とすると正弦定理より
\(R=AH=\sqrt{\displaystyle\frac{13}{3}}\)
したがって、\(△DAH\)で三平方の定理より
\(DH=\sqrt{3^2-(\displaystyle\frac{13}{3})^2}=\)\(\displaystyle\frac{\sqrt{42}}{3}\)
ゆえに、四面体\(ABCD\)の体積\(V\)は
\(V=\displaystyle\frac{1}{3}・△ABC・DH\)
\(=\displaystyle\frac{1}{3}・(\displaystyle\frac{1}{2}・3・4・\sin60°)・\displaystyle\frac{\sqrt{42}}{3}\)
\(=\sqrt{14}\)
(例題2)
四面体\(OABC\)は、
\(\angle BOC=\angle COA=\angle AOB=90°,OA=2,OB=\sqrt{2},OC=2\sqrt{2}\) である。
(1)この四面体の体積を求めよ。
(2)点\(O\)と平面\(ABC\)との距離を求めよ。
(1)
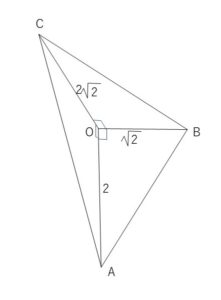
よって求める体積\(V\)は
\(V=\displaystyle\frac{1}{3}・△OBC・OA\)
\(=\displaystyle\frac{1}{3}・2・2\)
\(=\)\(\displaystyle\frac{4}{3}\)
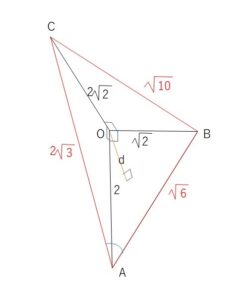
\(V=\displaystyle\frac{1}{3}・△ABC・h\)・・・①
\(AB=\sqrt{6},BC=\sqrt{10},CA=2\sqrt{3}\) であり、
\(△ABC\)において余弦定理より
\(\cos A=\displaystyle\frac{(\sqrt{6})^2+(2\sqrt{3})^2-(\sqrt{10})^2}{2・\sqrt{6}・2\sqrt{3}}=\displaystyle\frac{\sqrt{2}}{3}\)
\(0°<A<180°\) だから、\(\sin A=\sqrt{1-(\displaystyle\frac{\sqrt{2}}{3})^2}=\displaystyle\frac{\sqrt{7}}{3}\)
よって
\(△ABC=\displaystyle\frac{1}{2}・\sqrt{6}・2\sqrt{3}・\displaystyle\frac{\sqrt{7}}{3}=\sqrt{14}\)
したがって、①と(1)の結果から
\(\displaystyle\frac{4}{3}=\displaystyle\frac{1}{3}・\sqrt{14}・h\)
\(h=\displaystyle\frac{2\sqrt{14}}{7}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。