円錐に内接する球に関する問題を見ていきます。断面図を考えることで、円錐は三角形、球は円として考えことができます。
今まで空間図形から部分的に平面図形を取り出しましたが、今回の断面図も部分的に平面図形を取り出したものになります。
(問題)
頂点が\(A\)である、底面の半径\(2\)、母線の長さ\(6\)の円錐が、中心が\(O\)である球と側面で接し、底面の中心\(M\)でも接している。この球の半径を求めよ。
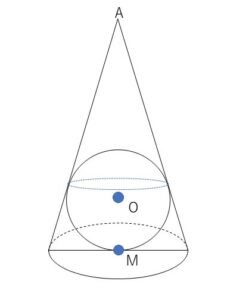
\(A\)と\(M\)を通る平面でズバッと切ります。そうすると、二等辺三角形に円が内接している断面図が得られます。イメージしずらい人は、断面図を\(AM\)を軸として回転させてみて下さい。そうすると二等辺三角形は円錐に、円は球になります。(球が内接もしてます)
内接円の半径が球の半径となるので、内接円の半径を求めることになりますが、3つの三角形に分けて、その和が全体の三角形になることを利用します。
(解答)
頂点\(A\)と底面の中心\(M\)を通る平面で立体を切ると断面図は次のようになる。
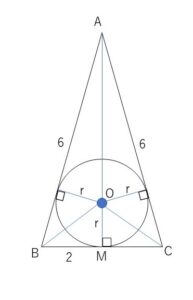
図のように\(B,C\)を定めると
\(AM=\sqrt{6^2-2^2}=4\sqrt{2}\) であるから
\(△ABC=\displaystyle\frac{1}{2}・4・4\sqrt{2}=8\sqrt{2}\)
球の半径を\(r\)とすると、図の円の半径も\(r\)なので
\(△ABC=△OAB+△OBC+△OCA\)
\(=\displaystyle\frac{1}{2}r(AB+BC+CA)\)
よって
\(8\sqrt{2}=\displaystyle\frac{1}{2}r(6+4+6)\)
\(r\)について解くと
\(r=\sqrt{2}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。