三角関数のグラフの平行移動・拡大縮小について見ていきます。
・グラフの平行移動
三角関数に限らず、関数\(y=f(x)\)のグラフを \(x\)軸方向に\(p\),\(y\)軸方向\(q\)平行移動したグラフの方程式は
\(y-q=f(x-p)\)
となります。
(証明)
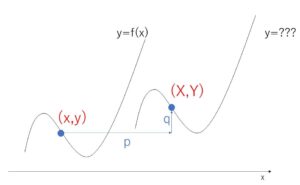
\(y=f(x)\)・・・①上の点を \((x,y)\) とする。この点を平行移動した先の点を\((X,Y)\)とすると、
\(X=x+p\)・・・② \(Y=y+q\)・・・③
②③より
\(x=X-p\), \(y=Y-q\)
これらを①に代入して
\(Y-q=f(X-p)\)・・・④
④が平行移動後のグラフの方程式となり、\(X→x\), \(Y→y\) とすれば目的の式が得られる。
・グラフの拡大縮小
三角関数に限らず
\(k>0\) のとき
\(y=f(x)\)を \(y\)軸方向に\(k\)倍,拡大縮小したグラフの方程式は
\(\displaystyle\frac{y}{k}=f(x)\) (\(y=kf(x)\))
となります。
また、\(y=f(x)\) を \(x\)軸方向に\(k\)倍,拡大縮小したグラフの方程式は
\(y=f(\displaystyle\frac{x}{k})\)
となります。
\(k<0\) のときは、拡大縮小にさらに\(x\)軸や\(y\)軸の対称移動が加わります。
(証明)
まずは\(y\)軸方向から。
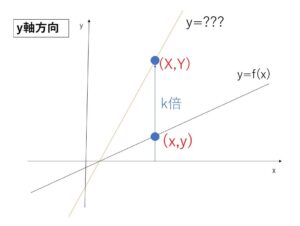
\(y=f(x)\)・・・① 上の点\((x,y)\)を\(y\)軸方向に\(k\)倍した点を\((X,Y)\)とすると
\(X=x\)・・・② \(Y=ky\)・・・③
②③より
\(x=X\), \(y=\displaystyle\frac{Y}{k}\)
これらを①に代入して
\(\displaystyle\frac{Y}{k}=f(X)\)
\(X→x\), \(Y→y\) にすれば目的の式が得られる。
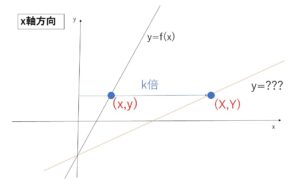
\(x\)軸方向も同様に移動後の点\((X,Y)\)について
\(X=kx\), \(Y=y\) より①に代入して
\(Y=f(\displaystyle\frac{X}{k})\)
\(X→x\), \(Y→y\) にすれば目的の式が得られる。
例えば、\(y=f(2x)\)は \(y=f(x)\)を\(x\)軸方向に2倍拡大したものではなく、\(\displaystyle\frac{1}{2}\)倍に縮小したものです。
\(y=f(\displaystyle\frac{1}{2}x)\)が\(x\)軸方向に2倍拡大したものです。
(例題)
\(y=3\sin(2θ+\displaystyle\frac{π}{3})\)・・・(ア) について
(1)(ア)のグラフは、\(y=\sinθ\) のグラフをどのように平行移動、拡大縮小したものか。
(2)(ア)の周期を求めよ。
\(y=3\sin2(θ+\displaystyle\frac{π}{6})\) です。
\(y=\sinθ\) → \(y=3\sin2θ\) → \(y=3\sin2(θ+\displaystyle\frac{π}{6})\) と順番に考えていきます。
(解答)
(1)
\(y=3\sin2(θ+\displaystyle\frac{π}{6})\)・・・(ア)
\(y=\sinθ\) を
\(θ\)軸方向に\(\displaystyle\frac{1}{2}\)倍縮小し
\(y\)軸方向に3倍拡大すると
\(y=3\sin2θ\)・・・(イ)
(イ)を\(θ\)軸方向に\(-\displaystyle\frac{π}{6}\) 平行移動すると
\(y=3\sin2(θ+\displaystyle\frac{π}{6})\)
答 \(θ\)軸方向に\(\displaystyle\frac{1}{2}\)倍縮小、\(y\)軸方向に3倍拡大して、\(θ\)軸方向に\(-\displaystyle\frac{π}{6}\) 平行移動したもの
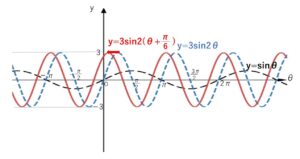
(イ)を\(θ\)軸方向に\(-\displaystyle\frac{π}{3}\) 平行移動したものは
\(y=3\sin2(θ+\displaystyle\frac{π}{3})\)\(=3\sin(2θ+\displaystyle\frac{2π}{3})\) で問題文の(ア)にはなりません。
(2)
よって \(y=3\sin2θ\) の周期を考えればよいことになります。
グラフを平行移動しても周期は変わらないので(1)より
\(y=3\sin2θ\) の周期を考えればよい。
\(y=3\sin2θ=f(θ)\)、周期を\(p\)とすれば
\(f(θ+p)=f(θ)\) が\(θ\)の値によらず成り立つ\(p\)を求めればよい。
\(3\sin2(θ+p)=3\sin2θ\)
\(\sin2(θ+p)=\sin2θ\)・・・(ウ)
(ウ)は結局 \(y=\sin2θ\) の周期を考えていることになる。
\(y=\sin2θ\) のグラフは、\(y=\sinθ\) のグラフを\(θ\)軸方向に\(\displaystyle\frac{1}{2}\)倍縮小しているので、周期は\(y=\sinθ\)の\(\displaystyle\frac{1}{2}\)となる。
よって周期は \(2π×\displaystyle\frac{1}{2}=\)\(π\)
係数が何であっても約分されるので、\(y\)軸方向の拡大縮小も周期には無関係になります。(感覚的にも縦方向の拡大縮小(引き伸ばし)は周期には関係なさそうと感じる)
結局\(θ\)の係数だけに着目すればよいことになります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角方程式・不等式①(基礎) back→三角関数のグラフ①