三角関数を含む方程式・不等式について見ていきます。
角が拡張されただけで、やることは三角比のときと同じです。
まずは三角方程式から
(例題1)次の三角方程式を解け。
(1) \(\sqrt{2}\sinθ=-1\) (\(0≦θ<2π\))
(2) \(\cosθ-1=0\) (\(θ\)は一般角)
(3) \(\sqrt{3}\tanθ+3=0\) (\(0≦θ<2π\))
(解答)
(1)
\(\sqrt{2}\sinθ=-1\) より
\(\sinθ=-\displaystyle\frac{1}{\sqrt{2}}\)
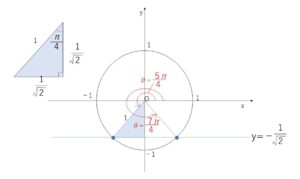
よって、単位円と\(y=-\displaystyle\frac{1}{\sqrt{2}}\) の交点\(P\)(2個ある)について、動径\(OP\)の角を求めればよいことになります。
単位円と\(y=-\displaystyle\frac{1}{\sqrt{2}}\) の交点について考えると、(\(0≦θ<2π\))と 図より
\(θ=\displaystyle\frac{5}{4}π,\displaystyle\frac{7}{4}π\)
(2)
\(\cosθ-1=0\) より
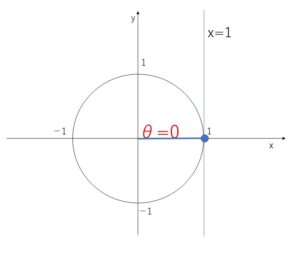
\(\cosθ=1\)・・・①
①を満たす角の1つは \(θ=0\) だから解(一般角)は
\(θ\)\(=0+2nπ\)\(=2nπ\) (\(n\)は整数)
(3)
\(\tanθ\)は動径の傾きなので、\(x,y\)座標の比に着目します。
\(\sqrt{3}\tanθ+3=0\) より
\(\sqrt{3}\tanθ=-3\)
よって
\(\tanθ=-\sqrt{3}\)
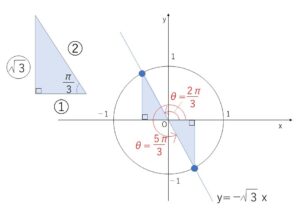
\(y=-\sqrt{3}x\) と単位円の交点を考えると、図より動径の表す角は\(0≦θ<2π\) から
\(θ=\displaystyle\frac{2}{3}π,\displaystyle\frac{5}{3}π\)
次に三角不等式です。
(例題2)
\(0≦θ<2π\) のとき、次の不等式を解け。
(1) \(2\sinθ<1\)
(2) \(2\cosθ+1>0\)
(3) \(\sqrt{3}\tanθ<1\)
あとは不等号を満たす範囲を図(単位円)より判断します。
(解答)
(1)
\(2\sinθ<1\) より
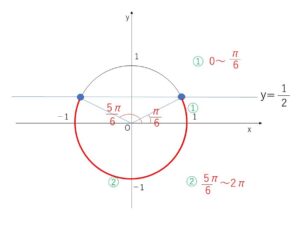
\(\sinθ<\displaystyle\frac{1}{2}\) (単位円上の点の\(y\)座標が\(\displaystyle\frac{1}{2}\)より小さい)
\(\sinθ=\displaystyle\frac{1}{2}\) を解くと
\(θ=\displaystyle\frac{π}{6},\displaystyle\frac{5}{6}π\)
よって、\(\sinθ<\displaystyle\frac{1}{2}\)の解は
\(0≦θ<\displaystyle\frac{π}{6}\), \(\displaystyle\frac{5}{6}π<θ<2π\)
(2)
\(2\cosθ+1>0\) より
\(2\cosθ>-1\)
\(\cosθ>-\displaystyle\frac{1}{2}\) (単位円上の点の\(x\)座標が\(-\displaystyle\frac{1}{2}\)より大きい)
\(\cosθ=-\displaystyle\frac{1}{2}\) を解くと
\(θ=\displaystyle\frac{2}{3}π,\displaystyle\frac{4}{3}π\)
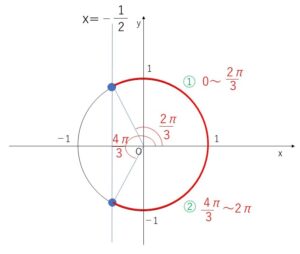
よって\(\cosθ>-\displaystyle\frac{1}{2}\) を満たす\(θ\)は図より
\(0≦θ<\displaystyle\frac{2}{3}π\), \(\displaystyle\frac{4}{3}π<θ<2π\)
(3)
\(\sqrt{3}\tanθ<1\) より
\(\tanθ<\displaystyle\frac{1}{\sqrt{3}}\) (動径の傾きが\(\displaystyle\frac{1}{\sqrt{3}}\)より小さい)
\(\tanθ=\displaystyle\frac{1}{\sqrt{3}}\) の解は
\(θ=\displaystyle\frac{π}{6},\displaystyle\frac{7}{6}π\)
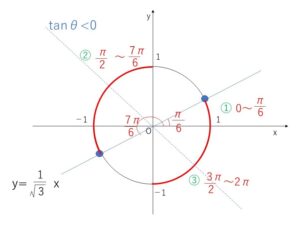
よって図より求める範囲は
\(0≦θ<\displaystyle\frac{π}{6}\), \(\displaystyle\frac{π}{2}<θ<\displaystyle\frac{7}{6}π\), \(\displaystyle\frac{3}{2}π<θ<2π\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角方程式・不等式② back→三角関数のグラフ②