2次式などの三角関数の問題について見ていきます。
(例題)
次の三角方程式・不等式を解け。
(1)\(2\sin^2θ-\sin(\displaystyle\frac{π}{2}+θ)\)\(-2\)\(=0\) (\(0≦θ≦π\))
(2)\(2\cos^2x+\sqrt{3}\sin x+1>0\) (\(0≦x<2π\))
(解答)
(1)
\(2\sin^2θ-\cosθ\)\(-2\)\(=0\)
となるので、今度は\(\cosθ\)に統一するために、\(\sin^2θ\)を\(\cos^2θ\)を使って変形します。
(\(\sinθ\)に統一しようとすると、\(\cosθ\)\(=±\sqrt{1-\sin^2θ}\) となりかなり面倒)
\(\sin(\displaystyle\frac{π}{2}+θ)\)\(=\cosθ\)
\(\sin^2θ=1-\cos^2θ\) より、与式は
\(2(1-\cos^2θ)-\cosθ\)\(-2\)\(=0\)
整理して
\(2\cos^2θ+\cosθ=0\)
\(\cosθ(2\cosθ+1)=0\)
よって
\(\cosθ=0,-\displaystyle\frac{1}{2}\)
\(0≦θ≦π\) のとき
\(\cosθ=0\) より \(θ=\displaystyle\frac{π}{2}\)
\(\cosθ=-\displaystyle\frac{1}{2}\) より \(θ=\displaystyle\frac{2}{3}π\)
答え \(θ=\displaystyle\frac{π}{2},\displaystyle\frac{2}{3}π\)
(2)
\(2\cos^2x+\sqrt{3}\sin x+1>0\) より
\(2(1-\sin^2x)+\sqrt{3}\sin x+1>0\)
整理して
\(2\sin^2x-\sqrt{3}\sin x-3<0\)
\((2\sin x+\sqrt{3})(\sin x-\sqrt{3})<0\)・・・①
①の \(\sin x-\sqrt{3}\)のほうは、\(-1≦\sin x≦1\) より必ず負の値になるから、
\(2\sin x+\sqrt{3}>0\) 。
ここで、\(\sin x-\sqrt{3}<0\) だから
\(2\sin x+\sqrt{3}>0\)
よって
\(\sin x>-\displaystyle\frac{\sqrt{3}}{2}\)・・・②
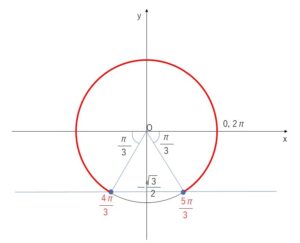
\(\sin x=-\displaystyle\frac{\sqrt{3}}{2}\) の解は、\(0≦x<2π\) で
\(x=\displaystyle\frac{4}{3}π,\displaystyle\frac{5}{3}π\)
したがって \(0≦x<2π\) で②を満たす\(x\)の範囲は
\(0≦x<\displaystyle\frac{4}{3}π\), \(\displaystyle\frac{5}{3}π<x<2π\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→加法定理①(証明) back→三角方程式・不等式②